KKMishra's Tutorials: Solutions to Problems on "GRAVITATION" - H C Verma's Concepts of Physics, Part-I, Chapter-11, Questions for Short Answer

My Channel on YouTube → SimplePhysics with KK

For links to

other chapters - See bottom of the page

GRAVITATION:--
QUESTIONS FOR SHORT ANSWER

1. Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?

ANSWER: If stationary, the net force on each of the two particles will not be zero, and they will exert the gravitational force on each other. So they will move towards each other and not be in equilibrium. If moving around their center of mass, they may maintain the relative distance as the gravitational force on each of the particles is balanced by the centrifugal force and the net force is zero.

Again for the same reason, three particles cannot be in equilibrium if stationary. If moving, they may maintain their relative distances for some configurations, again the gravitational force is balanced by centrifugal force.

One of the three particles can be in equilibrium even without moving. This situation can happen if two of the particles are moving around the center of mass and the third particle is stationary at the center of mass.

2. Is there any meaning of "Weight of the earth"?

ANSWER: No. Because the weight is the force by which the earth attracts a body. So the weight of the earth itself has no meaning.

3. If heavier bodies are attracted more strongly by the earth, why don't they fall faster than the lighter bodies?

ANSWER: The heavier bodies are attracted more strongly by the earth means the force applied by the earth is more. This force is the weight of the body = mg. Hence the acceleration of the body = force/mass = mg/m =g, which is independent of m. So all bodies fall with the same acceleration 'g'.

4. Can you think of two particles which do not exert a gravitational force on each other?

ANSWER: No. Since the particles have mass, they will exert a gravitational force on each other.

5. The earth revolves round the sun because the sun attracts the earth. The sun also attracts the moon and this force is about twice as large as the attraction of the earth on the moon. Why does the moon not revolve round the sun? Or does it?

ANSWER: The moon too revolves around the sun along with the earth.

6. At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight the sun and the earth pull these objects in the same direction. Is the weight of an object, as measured by a spring balance on the earth's surface, more at midnight as compared to its weight at noon?

ANSWER: The distance of the sun from the earth is R = 150x10⁶ km while the diameter of the earth is 12800 km only. So the variance of distance R between the noon and the midnight is comparatively very small (about 0.0085%). The force on an object by the sun is inversely proportional to R², so the change in the force between the noon and the midnight is even smaller or say negligible. So, the weight measured by a spring balance at the earth's surface at these two times will not differ as the spring balances are not sensitive enough to detect such negligible changes.

7. An apple falls from a tree. An insect in the apple finds that the earth is falling towards it with an acceleration g. Who exerts the force needed to accelerate the earth with this acceleration g?

ANSWER: From the observation of the insect, his frame of reference is noninertial. With the frame moving with an acceleration g, we will have to apply a pseudo force Mg on the earth in the opposite direction of g, if we want to use Newton's laws in this noninertial frame. So from the insect's view, this force is being exerted by the apple on the earth though it is not correct.

8. Suppose the gravitational potential due to a small system is k/r² at a distance r from it. What will be the gravitational field? Can you think of any such system? What happens if there were negative masses?

ANSWER: The gravitational potential V = k/r².

Hence gravitational field E = - dV/dr = -(-2k/r³) = 2k/r³

A hypothetical gravitational dipole system can be assumed like this, as in the case of an electric dipole in which the electric field is inversely proportional to the cube of the distance. It is hypothetical because in the case of gravitation negative masses do not occur.

If there were negative masses the direction of the field would be reversed.

9. The gravitational potential energy of a two-particle system is derived in this chapter as U = -Gm₁m₂/r. Does it follow from the equation that the potential energy for r = ∞ must be zero? Can we choose the potential energy for r = ∞ to be 20 J and still use this formula? If no, what formula should be used to calculate the gravitational potential energy at separation r?

ANSWER: Yes. Since U is inversely proportional to r, at r = ∞ the gravitational potential energy must be zero.

If we choose the potential energy at r = ∞ to be 20 J, we can not use this formula, because putting r = ∞, will not give the result 20 J.

The required formula will be,
U = -Gm₁m₂/r + 20.

10. The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at the equator and sell them at the poles? Does it matter whether a spring balance is used or an equal beam balance is used?

ANSWER: The weight of an object is about 0.50% (Very roughly) more at poles than at the equator. Though it seems beneficial at a glance to purchase goods at the equator and sell them at the poles, there are many factors which prove just the opposite. First, the input cost will become much higher than 0.50% in transporting them to a distant (9000+ km) and difficult place like poles. Second, there is no population on the poles, hence no purchaser and no market. Again the change in weight is noticeable only in a spring balance. No change in weight will be there if the equal beam balance is used because it compares the weight of an object to a standard weight and the increase in weight at poles will be same for the object and the standard weight.

11. The weight of the body at poles is greater than the weight at the equator. Is it the actual weight or the apparent weight we are talking about? Does your answer depend on whether only the earth's rotation is taken into account or the flattening of the earth at the poles is also taken into account?

ANSWER: The weight at the equator is the apparent weight which is affected by the earth's rotation and flattening of the earth at the poles. At poles, it is maximum and unaffected by these two reasons.

12. If the radius of the earth decreases by 1% without changing its mass, will the acceleration due to gravity at the surface of the earth increase or decrease? If so by what percent?

ANSWER: The mass of the earth can be considered concentrated at its center for calculation of the force between the earth and the object on or beyond its surface. With the mass of the earth being the same if the radius decreases by 1% it means the distance between the earth and the object reduces by 1%, other things being the same. Since the acceleration due to gravity is inversely proportional to the square of the radius of the earth R, the decrease in R will result in an increase in g.

The 1% decrease in R means it decreases by 0.99 times. So, the increase in g will be 1/(0.99)² = 1.02 times. That means the value of g increases by 2%.

13. A nut becomes loose and gets detached from a satellite

revolving around the earth. Will it land on the earth? If yes, where will it land? If no, how can an astronaut make it land on the earth?

ANSWER: No it will not land on the earth. It will orbit the earth like the satellite.

The astronaut will have to make its speed roughly towards the earth instead of the tangential speed.

14. Is it necessary for the plane of the orbit of a satellite to pass through the center of the earth?

ANSWER: Yes. Because the centripetal force on the satellite is towards the center of the earth where the earth's mass is apparently considered to be concentrated.

15. Consider earth satellites in circular orbits. A geostationary satellite must be at a height of about 36000 km from the earth's surface. Will any satellite moving at this height be a geostationary satellite? Will any satellite moving at this height have a time period of 24 hours?

ANSWER: No, only the satellites at this height moving over the equator and having the direction of rotation same as that of the earth will be geostationary and they will appear to be fixed at a place when viewed from the earth.

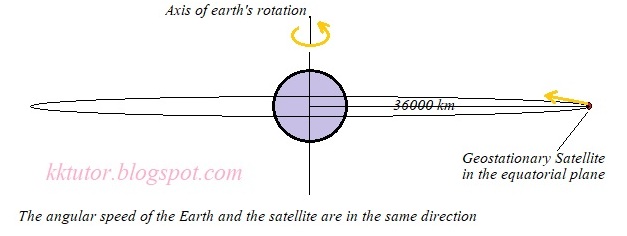A geostationary satellite

Yes, any satellite moving at this height will have the actual time period of 24 hours though this may not appear from the earth's surface depending upon their orbit and the direction of the rotation.

16. No part of India is situated on the equator? Is it possible to have a geostationary satellite which always remains over New Delhi?

ANSWER: No.

17. As the earth rotates about its axis, a person living in his house at the equator goes in a circular orbit of radius equal to the radius of the earth. Why does he/she not feel weightless as a satellite passenger does?

ANSWER: To feel the weightlessness in a circular orbit around the earth, the person should orbit with such a speed so that the centrifugal force must be equal to the apparent weight of the person. For this condition g = v²/R at earth's surface. This gives,
v =√gR = √(9.8*6400000) = 7920 m/s = 7.92 km/s
So only going in the circular orbit at the surface of the earth is not sufficient for the weightlessness but his speed also should be 7.92 km/s which is not possible for a person even in a vehicle or plane. Also, the resistance of air on the surface will make the vehicle burn at this speed.

18. Two satellites going in the equatorial plane have almost same radii. As seen from the earth one move from east to west and the other from west to east. Will they have the same time period as seen from the earth? If not, which one will have less time period?

ANSWER: As seen from the earth, the apparent time period for both the satellite will be different due to the rotation of the earth. The earth rotates from west o east. So, the satellite moving from east to west will have greater relative angular speed, hence, will have less time period.

19. A spacecraft consumes more fuel in going from the earth to the moon than it takes for a return trip. Comment on the statement.

ANSWER: It is true because in the first case the spacecraft has to spend more fuel to escape from the gravitational field of the earth (which is more than the moon) and to enter moon's field. In the second case, the fuel spent on escaping the moon's gravitation is less because it is up to the lesser distance.

===<<<O>>>===

Links to the chapters -