My Channel on YouTube → SimplePhysics with KK
For links to
other chapters - See bottom of the page
Or click here → kktutor.blogspot.com
ROTATIONAL MECHANICS:--
OBJECTIVE - I
1. Let A be a unit vector along the axis of rotation of a purely rotating body and B be a unit vector along the velocity of a particle P of the body away from the axis. The values of A.B is
(a) 1 (b) -1 (c) 0 (d) None of these
ANSWER: (c)
Explanation: The directions of A and B will be perpendicular to each other. Hence A.B = |A|.|B|.Cos90° =0.
2. A body is uniformly rotating about an axis fixed in an inertial frame of reference. Let A be a unit vector along the axis of rotation and B be the unit vector along the resultant force on a particle P of the body away from the axis. The value of A.B is
(a) 1 (b) -1 (c) 0 (d) None of these
ANSWER: (c)
Explanation: Since the body is uniformly rotating, the resultant force on the particle P will be in the radial direction. So again the directions of A and B will be perpendicular to each other. Hence A.B = |A|.|B|.Cos90° =0.
3. A particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
(a) is zero (b) remains constant
(c) goes on increasing (d) goes on decreasing
Explanation: Since the body is uniformly rotating, the resultant force on the particle P will be in the radial direction. So again the directions of A and B will be perpendicular to each other. Hence A.B = |A|.|B|.Cos90° =0.
3. A particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
(a) is zero (b) remains constant
(c) goes on increasing (d) goes on decreasing
ANSWER: (b)
Explanation: Since the particle moves with a constant velocity along a straight line, the distance of the line from the origin (r) remains constant. The linear momentum of the particle mv is constant. So the angular momentum of the particle about the origin = moment of the linear momentum about origin = mv.r = Constant.
4. A body is in pure rotation. The linear speed v of a particle, the distance r of the particle from the axis and the angular velocity ω of the body are related as ω = v/r. Thus
(a) ω ∝ 1/r (b) ω ∝ r
(c) ω = 0 (d) ω is independent of r.
Explanation: Since the particle moves with a constant velocity along a straight line, the distance of the line from the origin (r) remains constant. The linear momentum of the particle mv is constant. So the angular momentum of the particle about the origin = moment of the linear momentum about origin = mv.r = Constant.
4. A body is in pure rotation. The linear speed v of a particle, the distance r of the particle from the axis and the angular velocity ω of the body are related as ω = v/r. Thus
(a) ω ∝ 1/r (b) ω ∝ r
(c) ω = 0 (d) ω is independent of r.
ANSWER: (d)
Explanation: In fact, v ∝ r and ω is the constant of proportionality. Thus v = ω.r and since ω is a constant, so it is independent of r.
5. Figure (10-Q2) shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances traveled by A and B in the same time interval, then
(a) x= 2y (b) x =y (c) y = 2x (d) none of these
Explanation: In fact, v ∝ r and ω is the constant of proportionality. Thus v = ω.r and since ω is a constant, so it is independent of r.
5. Figure (10-Q2) shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances traveled by A and B in the same time interval, then
(a) x= 2y (b) x =y (c) y = 2x (d) none of these
 |
| Figure for Q-5 |
ANSWER: (c)
Explanation: Both the pulleys have same angular speed hence the speed of the string supporting B will be twice that of A because of the double radius. So it will cover twice distance than A in the same time interval.
6. A body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
(a) vertical (b) horizontal and skew with the axis
(c) horizontal and intersecting the axis
(d) none of these.
Explanation: Both the pulleys have same angular speed hence the speed of the string supporting B will be twice that of A because of the double radius. So it will cover twice distance than A in the same time interval.
6. A body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
(a) vertical (b) horizontal and skew with the axis
(c) horizontal and intersecting the axis
(d) none of these.
ANSWER: (c)
Explanation: Since the body is rotating uniformly, a particle not on the axis moves in a uniform circular motion. This circle will be horizontal with its center at the intersecting point with the axis. So it has a radial acceleration and hence a radial resultant force. Thus this force will be horizontal and intersecting the axis.
7. A body is rotating nonuniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
(a) vertical (b) horizontal and skew with the axis
(c) horizontal and intersecting the axis
(d) none of these.
Explanation: Since the body is rotating uniformly, a particle not on the axis moves in a uniform circular motion. This circle will be horizontal with its center at the intersecting point with the axis. So it has a radial acceleration and hence a radial resultant force. Thus this force will be horizontal and intersecting the axis.
7. A body is rotating nonuniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
(a) vertical (b) horizontal and skew with the axis
(c) horizontal and intersecting the axis
(d) none of these.
ANSWER: (b)
Explanation: Since the body is rotating nonuniformly about a vertical axis, a particle not on the axis will move on a circular path in a horizontal plane. It will have both radial and tangential accelerations and hence radial and tangential forces. The resultant force of these two mutually perpendicular forces will be in the horizontal plane but will not cross the axis.
8. Let F be a force acting on a particle having position vector r. Let Г be the torque of this force about the origin, then
(a) r.Г = 0 and F.Г = 0 (b) r.Г = 0 but F.Г ≠ 0
(c) r.Г ≠ 0 but F.Г ≠ 0 (d) r.Г ≠ 0 and F.Г ≠ 0
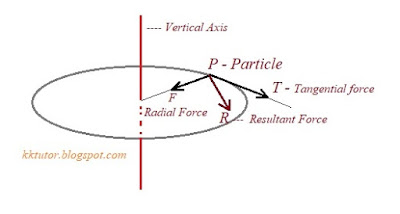 |
| Diagram for Q-7 |
Explanation: Since the body is rotating nonuniformly about a vertical axis, a particle not on the axis will move on a circular path in a horizontal plane. It will have both radial and tangential accelerations and hence radial and tangential forces. The resultant force of these two mutually perpendicular forces will be in the horizontal plane but will not cross the axis.
8. Let F be a force acting on a particle having position vector r. Let Г be the torque of this force about the origin, then
(a) r.Г = 0 and F.Г = 0 (b) r.Г = 0 but F.Г ≠ 0
(c) r.Г ≠ 0 but F.Г ≠ 0 (d) r.Г ≠ 0 and F.Г ≠ 0
ANSWER: (a)
Explanation: Г = r x F and the direction of Г is perpendicular to the plane containing r and F i.e. Г is perpendicular to both r and F. So r.Г = rГ.cos90° = 0 and F.Г = FГ.cos90° = 0
9. One end of a uniform rod of mass m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
(a) mω²l (b) zero (c) mg (d) ½mω²l.
Explanation: Г = r x F and the direction of Г is perpendicular to the plane containing r and F i.e. Г is perpendicular to both r and F. So r.Г = rГ.cos90° = 0 and F.Г = FГ.cos90° = 0
9. One end of a uniform rod of mass m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
(a) mω²l (b) zero (c) mg (d) ½mω²l.
ANSWER: (d)
Explanation: Since the rod rotates on the horizontal surface, the horizontal component of the force applied by the clamp is the centripetal force = mω²r = mω²(l/2) = ½mω²l.
10. A uniform rod is kept vertically on a horizontal smooth surface at a point O. If it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
(a) at O (b) at a distance less than l/2 from O
(c) at a distance l/2 from O
(d) at a distance larger than l/2 from O.
Explanation: Since the rod rotates on the horizontal surface, the horizontal component of the force applied by the clamp is the centripetal force = mω²r = mω²(l/2) = ½mω²l.
10. A uniform rod is kept vertically on a horizontal smooth surface at a point O. If it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
(a) at O (b) at a distance less than l/2 from O
(c) at a distance l/2 from O
(d) at a distance larger than l/2 from O.
ANSWER: (c)
Explanation: Since the rod is uniform its Center of mass (CoM) will be in the middle i.e. at l/2 distance from the ends. When the rod is vertical the CoM will bel/2 distance vertically above the point O. Since there is no force in the horizontal direction the CoM will be on the point O after it falls down. Hence the lower end will remain at a distance l/2 from O.
11. A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is
(a) IA > IB (b) IA = IB (c) IA < IB (d) depends on the actual value of t and r.
Explanation: Since the rod is uniform its Center of mass (CoM) will be in the middle i.e. at l/2 distance from the ends. When the rod is vertical the CoM will bel/2 distance vertically above the point O. Since there is no force in the horizontal direction the CoM will be on the point O after it falls down. Hence the lower end will remain at a distance l/2 from O.
11. A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is
(a) IA > IB (b) IA = IB (c) IA < IB (d) depends on the actual value of t and r.
ANSWER: (c)
Explanation: Let the density of iron plate be ρ.
Mass of first disc m = πr²tρ
M.I. = IA = ½mr² == ½πr²tρr² = ½πr4tρ
Mass of second disc = M = π(4r)²(t/4)ρ = 4πr²tρ
M.I. = IB = ½M(4r)² = ½4πr²tρ16r² = 32πr4tρ
Clearly, IA < IB.
12. Equal torques act on the discs A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are vA and vB respectively. We have
(a) vA > vB (b) vA = vB (c) vA < vB
(d) the relation depends on the actual magnitude of the torques.
Explanation: Let the density of iron plate be ρ.
Mass of first disc m = πr²tρ
M.I. = IA = ½mr² == ½πr²tρr² = ½πr4tρ
Mass of second disc = M = π(4r)²(t/4)ρ = 4πr²tρ
M.I. = IB = ½M(4r)² = ½4πr²tρ16r² = 32πr4tρ
Clearly, IA < IB.
12. Equal torques act on the discs A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are vA and vB respectively. We have
(a) vA > vB (b) vA = vB (c) vA < vB
(d) the relation depends on the actual magnitude of the torques.
ANSWER: (a)
Explanation: Let T be the torque and A and A' be the angular accelerations. A = T/IA and A' = T/IB. Clearly A >A'. In fact, the ratio of the moment of Inertias is 64. So at a later instant, the angular velocity of the first disc will be much greater than the second. Hence option (a).
13. A closed cylindrical tube containing some water (not filling the entire tube) lies in a horizontal plane. If the tube is rotated about a perpendicular bisector, the moment of inertia of water about the axis
(a) increases (b) decreases (c) remains constant (d) increases if the rotation is clockwise and decreases if it is anticlockwise.
Explanation: Let T be the torque and A and A' be the angular accelerations. A = T/IA and A' = T/IB. Clearly A >A'. In fact, the ratio of the moment of Inertias is 64. So at a later instant, the angular velocity of the first disc will be much greater than the second. Hence option (a).
13. A closed cylindrical tube containing some water (not filling the entire tube) lies in a horizontal plane. If the tube is rotated about a perpendicular bisector, the moment of inertia of water about the axis
(a) increases (b) decreases (c) remains constant (d) increases if the rotation is clockwise and decreases if it is anticlockwise.
ANSWER: (a)
Explanation: During the above rotation water will move away from the axis of rotation. And the moment of inertia is directly proportional to the square of the distance of the mass from the axis of rotation. Hence the option (a).
14. The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the center is
(a) Mr² (b) ½Mr² (c) ¼Mr² (d) (2/5)Mr².
Explanation: During the above rotation water will move away from the axis of rotation. And the moment of inertia is directly proportional to the square of the distance of the mass from the axis of rotation. Hence the option (a).
14. The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the center is
(a) Mr² (b) ½Mr² (c) ¼Mr² (d) (2/5)Mr².
ANSWER: (a)
Explanation: Since the mass of the wire is at a distance r away from the axis. Hence the option (a).
15. Let I1 and I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminum and the second of iron.
(a) I1 < I2 (b) I1 = I2 (c) I1 > I2 (d) relation betwen I1 and I2 depends on the actual shape of the bodies.
Explanation: Since the mass of the wire is at a distance r away from the axis. Hence the option (a).
15. Let I1 and I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminum and the second of iron.
(a) I1 < I2 (b) I1 = I2 (c) I1 > I2 (d) relation betwen I1 and I2 depends on the actual shape of the bodies.
ANSWER: (a)
Explanation: Aluminum has a lower density than iron hence the first body has lesser mass than the second. And if the shapes of the bodies are same the M.I. is directly proportional to the mass. So the first body will have lower M.I. than the second body.
16. A body having its center of mass at the origin has three of its particle at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0.20 kg-m² each. The moment of inertia about the Z-axis
(a) is 0.20 kg-m² (b) 0.40 kg-m² (c) is 0.20/2 kg-m² (d) Cannot be deduced with the information.
Explanation: Aluminum has a lower density than iron hence the first body has lesser mass than the second. And if the shapes of the bodies are same the M.I. is directly proportional to the mass. So the first body will have lower M.I. than the second body.
16. A body having its center of mass at the origin has three of its particle at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0.20 kg-m² each. The moment of inertia about the Z-axis
(a) is 0.20 kg-m² (b) 0.40 kg-m² (c) is 0.20/2 kg-m² (d) Cannot be deduced with the information.
ANSWER: (d)
Explanation: To know the moment of inertia we need to know the mass and shape of the body. None is available in the problem, hence the option (d).
17. A cubical block of mass M and edge a slides down a rough inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its center has a magnitude
(a) zero (b) Mga (c) Mga.sinθ (d) ½Mga.sinθ.
Explanation: To know the moment of inertia we need to know the mass and shape of the body. None is available in the problem, hence the option (d).
17. A cubical block of mass M and edge a slides down a rough inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its center has a magnitude
(a) zero (b) Mga (c) Mga.sinθ (d) ½Mga.sinθ.
ANSWER: (d)
Explanation: See the diagram below.
The weight Mg of the cubical block can be resolved along the plane and perpendicular to it. Since the block is sliding down with a uniform velocity, the resultant force along the plane is zero. There are only two forces along the plane - Weight component (Mg.sinθ) and the force of friction F in the opposite direction.
F+Mg.sinθ =0
→F= - Mg.sinθ
So these two forces are equal and opposite in direction. But they are not in the same line. While the weight component acts through CoM, the Friction force acts along the contact surface. Since the edge of the block is 'a' it is clear that the distance between these two forces = a/2. The torque produced by these two forces = ½Mga.sinθ. In the figure, it is in the anti-clockwise direction.
Now consider the weight component perpendicular to the plane acting through the CoM which is balanced by the equal and opposite Normal Force N. But N is not in line with the perpendicular weight component i.e. it does not pass through the Com. These two equal and opposite forces create a torque in the clockwise direction and its magnitude is same as the first torque because the block does not have angular motion. So the torque produced by the normal force is equal to ½Mga.sinθ.
18. A thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become
(a) ωM/(M+m) (b) ωM/(M+2m) (c) ω(M-2m)/(M+2m) (d) ω(M+2m)/M
Explanation: See the diagram below.
 |
| Figure for Q-17 |
F+Mg.sinθ =0
→F= - Mg.sinθ
So these two forces are equal and opposite in direction. But they are not in the same line. While the weight component acts through CoM, the Friction force acts along the contact surface. Since the edge of the block is 'a' it is clear that the distance between these two forces = a/2. The torque produced by these two forces = ½Mga.sinθ. In the figure, it is in the anti-clockwise direction.
Now consider the weight component perpendicular to the plane acting through the CoM which is balanced by the equal and opposite Normal Force N. But N is not in line with the perpendicular weight component i.e. it does not pass through the Com. These two equal and opposite forces create a torque in the clockwise direction and its magnitude is same as the first torque because the block does not have angular motion. So the torque produced by the normal force is equal to ½Mga.sinθ.
18. A thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become
(a) ωM/(M+m) (b) ωM/(M+2m) (c) ω(M-2m)/(M+2m) (d) ω(M+2m)/M
ANSWER: (b)
Explanation: Moment of inertia of the ring I = Mr²
Angular Momentum = I⍵
When the masses are attached, the moment of Inertia I'= Mr²+2mr²
=(M+2m)r²
Let the new angular speed be ⍵'. So the angular momentum =I'⍵'.
Since the angular momentum is conserved. I'⍵'=I⍵
→⍵' = I⍵/I' =⍵Mr²/(M+2m)r² =⍵M/(M+2m)
19. A person sitting firmly over a rotating stool has his arms stretched. If he folds his arms, his angular momentum about the axis of rotation
(a) increases (b) decreases (c) remains unchanged (d) doubles
Explanation: Moment of inertia of the ring I = Mr²
Angular Momentum = I⍵
When the masses are attached, the moment of Inertia I'= Mr²+2mr²
=(M+2m)r²
Let the new angular speed be ⍵'. So the angular momentum =I'⍵'.
Since the angular momentum is conserved. I'⍵'=I⍵
→⍵' = I⍵/I' =⍵Mr²/(M+2m)r² =⍵M/(M+2m)
19. A person sitting firmly over a rotating stool has his arms stretched. If he folds his arms, his angular momentum about the axis of rotation
(a) increases (b) decreases (c) remains unchanged (d) doubles
ANSWER: (c)
Explanation: If there is no external torque, the angular momentum is conserved. It is true if the moment of inertia of the rotating part of the stool is negligible with respect to the man.
Note: As informed by one of the students in the comment section below, the answer in the latest edition is changed to (b) i.e. decreases. It is true if the moment of inertia of the stool is considered and it is considerable with respect to the moment of inertia of the man. The angular momentum of the man with the stool will remain unchanged. If the initial angular speed =⍵ and the final angular speed =⍵', then
(Iₘ+Iₛ)⍵ =(Iₘ'+Iₛ)⍵'
→Iₘ⍵ +Iₛ⍵ =Iₘ'⍵'+Iₛ⍵' = const. ------- (i)
{Iₘ and Iₘ' are initial and final M.I. of the man, Iₛ = M.I. of the stool}
When the man folds his hands, his moment of inertia decreases and hence the sum of M.I of man and the stool decreases (even though M.I. of the stool remains constant). To conserve the angular momentum the angular speed increases i.e. ⍵' > ⍵. So the angular momentum of the stool increases Iₛ⍵' > Iₛ⍵. Since the sum of the angular momentum of the stool and the man is constant the angular momentum of the man must decrease after folding his hands. As in (i), Iₘ'⍵' < Iₘ⍵.
20. The Center of a wheel rolling on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the center will be moving at a speed
(a) zero (b) v0 (c) √2v0 (d) 2v0.
Explanation: If there is no external torque, the angular momentum is conserved. It is true if the moment of inertia of the rotating part of the stool is negligible with respect to the man.
Note: As informed by one of the students in the comment section below, the answer in the latest edition is changed to (b) i.e. decreases. It is true if the moment of inertia of the stool is considered and it is considerable with respect to the moment of inertia of the man. The angular momentum of the man with the stool will remain unchanged. If the initial angular speed =⍵ and the final angular speed =⍵', then
(Iₘ+Iₛ)⍵ =(Iₘ'+Iₛ)⍵'
→Iₘ⍵ +Iₛ⍵ =Iₘ'⍵'+Iₛ⍵' = const. ------- (i)
{Iₘ and Iₘ' are initial and final M.I. of the man, Iₛ = M.I. of the stool}
When the man folds his hands, his moment of inertia decreases and hence the sum of M.I of man and the stool decreases (even though M.I. of the stool remains constant). To conserve the angular momentum the angular speed increases i.e. ⍵' > ⍵. So the angular momentum of the stool increases Iₛ⍵' > Iₛ⍵. Since the sum of the angular momentum of the stool and the man is constant the angular momentum of the man must decrease after folding his hands. As in (i), Iₘ'⍵' < Iₘ⍵.
20. The Center of a wheel rolling on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the center will be moving at a speed
(a) zero (b) v0 (c) √2v0 (d) 2v0.
ANSWER: (c)
Explanation: Let the radius of the wheel = r.
The angular speed of the wheel ⍵ = v0/r
A particle on the rim of the wheel at the same level as the center will have a vertical speed =⍵r =(v0/r)*r = v0 and a horizontal speed = v0
So the resultant speed =√(v0²+v0²) =√(2v0²) =√2v0
21. A wheel of radius 20 cm is pushed to move it on a rough horizontal surface. It is found to move through a distance of 60 cm on the road during the time it completes one revolution about the center. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is
(a) along the velocity of the wheel
(b) opposite to the velocity of the wheel
(c) perpendicular to the velocity of the wheel
(d) zero
Explanation: Let the radius of the wheel = r.
The angular speed of the wheel ⍵ = v0/r
A particle on the rim of the wheel at the same level as the center will have a vertical speed =⍵r =(v0/r)*r = v0 and a horizontal speed = v0
So the resultant speed =√(v0²+v0²) =√(2v0²) =√2v0
21. A wheel of radius 20 cm is pushed to move it on a rough horizontal surface. It is found to move through a distance of 60 cm on the road during the time it completes one revolution about the center. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is
(a) along the velocity of the wheel
(b) opposite to the velocity of the wheel
(c) perpendicular to the velocity of the wheel
(d) zero
ANSWER: (a)
Explanation: Perimeter of the wheel = 2π*0.20 =0.4π =1.26 m
But it moves only 0.60 m.
So the wheel slips on the road. At the point of contact with the road, the part of the wheel is sliding backward. Hence the force of friction acts forward i.e. along the velocity of the wheel.
22. The angular velocity of the engine (and hence of the wheel) of a scooter is proportional to the petrol input per second. The scooter is moving at a frictionless road with uniform velocity. If the petrol input is increased by 10%, the linear velocity of the scooter is increased by
(a) 50% (b) 10% (c) 20% (d) 0%
Explanation: Perimeter of the wheel = 2π*0.20 =0.4π =1.26 m
But it moves only 0.60 m.
So the wheel slips on the road. At the point of contact with the road, the part of the wheel is sliding backward. Hence the force of friction acts forward i.e. along the velocity of the wheel.
22. The angular velocity of the engine (and hence of the wheel) of a scooter is proportional to the petrol input per second. The scooter is moving at a frictionless road with uniform velocity. If the petrol input is increased by 10%, the linear velocity of the scooter is increased by
(a) 50% (b) 10% (c) 20% (d) 0%
ANSWER: (d)
Explanation: With the increase of petrol input the angular velocity of the wheel increases but in the absence of friction on the road, no external force on the scooter is applied. Hence the linear velocity of the scooter is not increased.
23. A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of a smooth incline and released. Least time will be taken in reaching the bottom by
(a) the solid sphere (b) the hollow sphere
(c) the disc (d) all will take same time.
Explanation: With the increase of petrol input the angular velocity of the wheel increases but in the absence of friction on the road, no external force on the scooter is applied. Hence the linear velocity of the scooter is not increased.
23. A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of a smooth incline and released. Least time will be taken in reaching the bottom by
(a) the solid sphere (b) the hollow sphere
(c) the disc (d) all will take same time.
ANSWER: (d)
Explanation: Since there is no friction on the incline, the only force on each of these objects along the incline is their weight component mg.sinθ.
So each of them have same initial velocity=0 and same acceleration=mg.sinθ/m = g.sinθ
So the time taken by each of them t is given by
S=0*t+½g.sinθ*t²
t²=2S/g.sinθ
t=√{2S/g.sinθ}
where S is the length of the incline.
24. A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
(a) the solid sphere (b) the hollow sphere
(c) the disc (d) all will take same time.
Explanation: Since there is no friction on the incline, the only force on each of these objects along the incline is their weight component mg.sinθ.
So each of them have same initial velocity=0 and same acceleration=mg.sinθ/m = g.sinθ
So the time taken by each of them t is given by
S=0*t+½g.sinθ*t²
t²=2S/g.sinθ
t=√{2S/g.sinθ}
where S is the length of the incline.
24. A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
(a) the solid sphere (b) the hollow sphere
(c) the disc (d) all will take same time.
ANSWER: (d)
Explanation: Since pure rolling does not occur, the objects slide. Therefore on each of them, a frictional force acts against the motion. Now, the normal force on each of the objects =mg.cosθ.
Frictional force = µ*mg.cosθ
Net force along the incline = mg.sinθ -µ*mg.cosθ
= m(g.sinθ -µg.cosθ)
Acceleration of each of the block = m(g.sinθ -µg.cosθ)/m
= (g.sinθ -µg.cosθ)
25. In the previous question, the smallest kinetic energy at the bottom of the incline will be achieved by
(a) the solid sphere (b) the hollow sphere
(c) the disc (d) all will achieve same kinetic energy.
Explanation: Since pure rolling does not occur, the objects slide. Therefore on each of them, a frictional force acts against the motion. Now, the normal force on each of the objects =mg.cosθ.
Frictional force = µ*mg.cosθ
Net force along the incline = mg.sinθ -µ*mg.cosθ
= m(g.sinθ -µg.cosθ)
Acceleration of each of the block = m(g.sinθ -µg.cosθ)/m
= (g.sinθ -µg.cosθ)
Since the accelerations and the initial velocities are same the time taken to reach the bottom will be the same for all objects.
Time can be calculated as in the previous explanation.
25. In the previous question, the smallest kinetic energy at the bottom of the incline will be achieved by
(a) the solid sphere (b) the hollow sphere
(c) the disc (d) all will achieve same kinetic energy.
ANSWER: (b)
Explanation: Since all objects reach the bottom at the same time, so their velocities are also the same hence same K.E. due to linear velocity.
Since each has the same radius and acted upon by equal forces, the torque on each of them is also the same. But the moment of Inertia is different for them. Since the mass is the most away from the center in the hollow sphere (or may say that the radius of gyration is greater for the hollow sphere) its M.I. is greater. Therefore it will have the smallest angular speed.
Rotational K.E. ∝ ω²
Hence it will have the smallest K.E.
26. A string of negligible thickness is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the string and pulls the cylinder towards him (figure 10-Q3). There is no slipping anywhere. The length of the string passed through the hand of the man while the cylinder reaches his hands is
(a) l (b) 2l (c) 3l (d) 4l
Explanation: Since all objects reach the bottom at the same time, so their velocities are also the same hence same K.E. due to linear velocity.
Since each has the same radius and acted upon by equal forces, the torque on each of them is also the same. But the moment of Inertia is different for them. Since the mass is the most away from the center in the hollow sphere (or may say that the radius of gyration is greater for the hollow sphere) its M.I. is greater. Therefore it will have the smallest angular speed.
Rotational K.E. ∝ ω²
Hence it will have the smallest K.E.
26. A string of negligible thickness is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the string and pulls the cylinder towards him (figure 10-Q3). There is no slipping anywhere. The length of the string passed through the hand of the man while the cylinder reaches his hands is
(a) l (b) 2l (c) 3l (d) 4l
 |
| Figure for Q-26 |
ANSWER: (b)
Explanation: Consider a vertical diameter of the cylinder. While rolling, at any instant, the lowest point of the diameter is in contact with the surface and does not move, The center moves a certain distance say x, and the top-most point of the diameter moves twice that = 2x. So when the center of the cylinder moves a distance l, the string length that unfolds through the top = 2l.
Explanation: Consider a vertical diameter of the cylinder. While rolling, at any instant, the lowest point of the diameter is in contact with the surface and does not move, The center moves a certain distance say x, and the top-most point of the diameter moves twice that = 2x. So when the center of the cylinder moves a distance l, the string length that unfolds through the top = 2l.
===<<<O>>>===
Links to the chapters -
ALL LINKS
CHAPTER- 10 - Rotational Mechanics
Questions for Short Answers
OBJECTIVE - I
OBJECTIVE - II
EXERCISES - Q-1 TO Q-15
EXERCISES - Q-16 TO Q-30
CHAPTER- 10 - Rotational Mechanics
Questions for Short Answers
OBJECTIVE - I
OBJECTIVE - II
EXERCISES - Q-1 TO Q-15
EXERCISES - Q-16 TO Q-30
CHAPTER- 9 - Center of Mass, Linear Momentum, Collision
HC Verma's Concepts of Physics, Chapter-8, WORK AND ENERGY
Click here for → Question for Short Answers
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → Exercises (1-10)
Click here for → Exercises (11-20)
Click here for → Exercises (21-30)
Click here for → Exercises (31-42)
Click here for → Exercise(43-54)
Click here for → Exercises (31-42)
Click here for → Exercise(43-54)
HC Verma's Concepts of Physics, Chapter-7, Circular Motion
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-30)
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-30)
HC Verma's Concepts of Physics, Chapter-6, Friction
Click here for → Friction OBJECTIVE-I
Click here for → Friction - OBJECTIVE-II
Click here for → Friction - OBJECTIVE-II
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
---------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-5, Newton's Law's of Motion
Click here for → QUESTIONS FOR SHORT ANSWER
Click here for→ Newton's laws of motion - Objective - I
Click here for → Newton's Laws of Motion - Objective -II
Click here for → Newton's Laws of Motion-Exercises(Q. No. 1 to 12)
Click here for→Newton's Laws of Motion,Exercises(Q.No. 13 to 27)
-------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-4, The Forces
"Questions for short Answers"
Click here for "The Forces" - OBJECTIVE-I
Click here for "The Forces" - OBJECTIVE-II
Click here for "The Forces" - Exercises
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------
Pls recheck solution of ques 9 ,radius is L not L/2
ReplyDeleteThe mass of the rod can be assumed to be concentrated at its centre of mass. Since the rod is uniform, its centre of mass will be in the middle of the rod. So the distance of CoM from the clamp = L/2.
DeleteDear sir,
ReplyDeleteIn objective - I, question 19, in latest edition, the answer has been changed to 'decreases' i.e 'b'. Detailed explanation is given at: http://www.concepts-of-physics.com/dr-hc-verma/errors-in-cop.php
Dear student, when the man is considered without the rotating part of the stool, theoretically the answer (b) is correct.If the M.I. of the stool is considerable with respect to the man, the the answer (b) is undoubtedly correct.
DeleteI think when initially the question was thought, they did not think of the moving part of the stool separately. That is why the answer (c) remained in prints so many long years.
Thanks for the information. I will insert it in the answer.