H C Verma solutions, Physics and Mathematics, Concepts of Physics - Part 1" - Chapter 2, OBJECTIVE-I

Objective - I

1. A vector is not changed if
   (a) It is rotated through an arbitrary angle
   (b) It is multiplied by an arbitrary scalar
   (c) It is cross-multiplied by a unit vector
   (d) It is slid parallel to itself

Answer: (d) 

Explanation: (d) is correct because if it is slid parallel to itself that does not change the direction or magnitude of the vector. In the case of (a) and (c) the direction of the vector changes while in the case of (b) magnitude of the vector changes.

2. Which of the sets given below may represent the magnitudes of three vectors adding to zero?
 (a) 2,4,8  (b) 4,8,16 (c) 1,2,1 (d) 0.5,1,2

Answer: (c) 

Explanation: (c) is correct answer because if the sum of three vectors is zero then their magnitudes represent a triangle and one of the properties of triangles is that sum of any two sides is greater than the third side. Options (a),(b) and (d) do not follow this condition so they can not form a triangle. In option (c) 1+1=2, so it is a special case of a triangle of which all three sides are collinear. See also the figure below:-

If resultant of three vectors is zero, their magnitudes represent the sides of a triangle

3. Resultant of A and B makes an angle α with A and β with B,
  (a) α<β 
  (b) α<β if  A < B 
  (c) α<β if  A ＞B 
  (d) α<β if  A = B 

Answer: (c) 

Explanation:  It will be clear from parallelogram law of addition of two vectors that the resultant makes a smaller angle with the greater vector.

The angle between a Vector and its resultant

4. The component of a vector is
  (a) Always less than its magnitude
  (b) Always greater than its magnitude
  (c) Always equal to its magnitude
  (d) None of these

Answer: (d)

Explanation:  The component of a vector may be less than, greater than or equal to its magnitude. It will be clear from the following figure.

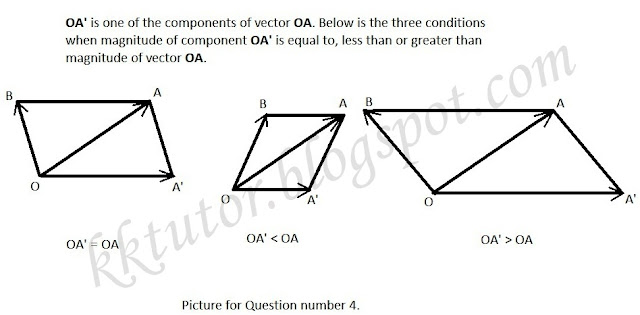The magnitude of the component of a Vector

5. A vector A points vertically upward and B points towards the north. The vector product A x B
  (a) along west
  (b) along east
  (c) zero
  (d) vertically downward.

Answer: (a)

Explanation:  The cross product A x B is a vector, direction of which will be perpendicular to the plane of A and B. Given the condition this direction may be along west or east. Using the right-hand rule it can be found that this is west.

The direction of a cross product of two vectors can be known by "Right-hand rule".

6. The radius of a circle is stated as 2.12 cm. Its area should be written as 
(a) 14 cm²
(b) 14.1 cm²
(c) 14.11 cm²
(d) 14.1124 cm² 

Answer: (b)

Explanation:  The area of circle A = π.r² 
π = 3.14, r = 2.12 cm. The minimum number of significant digits in this multiplication quantities is three, hence the result should also have three significant digits rounded.
A = 3.141*2.12*2.12 cm² = 14.1124 cm² =14.1 cm²
      Third significant digit is 1 which is to be rounded. Next to it is 1 which is less than 5. So the fourth digit onwards will be dropped and 14.1124 cm² rounded to three significant digits is 14.1 cm². 

===<<<O>>>=== 

My Channel on YouTube  →  SimplePhysics with KK

For links to 

other chapters - See bottom of the page

Or click here → kktutor.blogspot.com
For beginners - Vectors & its addition -YouTube

Links to the Chapters

ALL LINKS

CHAPTER- 18 - Geometrical Optics

Questions for Short Answers

CHAPTER- 17 - Light Waves

Questions for Short Answers

OBJECTIVE - I

OBJECTIVE - II

EXERCISES - Q1-Q10

EXERCISES - Q11-Q20

EXERCISES - Q21-Q30

EXERCISES - Q31-Q41

CHAPTER- 16 - Sound Waves

Questions for Short Answers

OBJECTIVE-I

OBJECTIVE-II

EXERCISES - Q-1 TO Q-10

EXERCISES - Q-11 TO Q-20

EXERCISES -Q-21 TO Q-30

EXERCISES -Q-31 TO Q-40

EXERCISES -Q-41 TO Q-50

EXERCISES -Q-51 TO Q-60

EXERCISES -Q-61 TO Q-70

EXERCISES - Q-71 TO Q-80

EXERCISES - Q-81 TO Q-89

CHAPTER- 15 - Wave Motion and Waves on a String

Questions for Short Answers

OBJECTIVE-I

OBJECTIVE-II

EXERCISES - Q-1 TO Q-10

EXERCISES - Q-11 TO Q-20

EXERCISES - Q-21 TO Q-30

EXERCISES - Q-31 TO Q-40

EXERCISES - Q-41 TO Q-50

EXERCISES - Q-51 TO Q-57 

CHAPTER- 14 - Fluid Mechanics

Questions for Short Answers

OBJECTIVE-I

OBJECTIVE-II

EXERCISES- Q-1 TO Q-10

EXERCISES- Q-11 TO Q-20

CHAPTER- 13 - Fluid Mechanics

Questions for Short Answers

OBJECTIVE-I

OBJECTIVE-II

EXERCISES Q-1 TO Q-10

EXERCISES- Q11 TO Q20

EXERCISES Q-21 TO Q30

EXERCISES Q-31 TO Q35

CHAPTER- 12 - Simple Harmonic Motion

Questions for Short Answers

OBJECTIVE-I

OBJECTIVE-II

EXERCISES- Q1 TO Q10

EXERCISES- Q11 TO Q20

EXERCISES- Q21 TO Q30

EXERCISES- Q31 TO Q40

EXERCISES- Q41 TO Q50

EXERCISES- Q51 TO Q58 (2-Extra Questions)

CHAPTER- 11 - Gravitation

Questions for Short Answers

OBJECTIVE - I

OBJECTIVE - II

EXERCISES - Q_1 to Q_10

EXERCISES -Q-11 TO Q-20

EXERCISES -Q 21 TO 30

EXERCISES -Q 31 TO 39

CHAPTER- 10 - Rotational Mechanics

Questions for Short Answers

OBJECTIVE - I

OBJECTIVE - II

EXERCISES - Q-1 TO Q-15

EXERCISES - Q-16 TO Q-30

EXERCISES Q-31 TO Q-45

EXERCISES Q-46 TO Q-60

EXERCISES Q-61 TO Q-75

EXERCISES Q-76 TO Q-86

CHAPTER- 9 - Center of Mass, Linear Momentum, Collision

Questions for Short Answers

Objective - I

Objective - II

EXERCISES Q-1 TO Q-10

EXERCISES Q-11TO Q-20

EXERCISES Q-21 TO Q-30

EXERCISES Q-31 TO Q-42

EXERCISES Q-43 TO Q-54

CHAPTER- 8 - Work and Energy

Click here for → Question for Short Answers

Click here for → OBJECTIVE-I

Click here for → OBJECTIVE-II

Click here for → Exercises (1-10)

Click here for → Exercises (11-20)

Click here for → Exercises (21-30)

Click here for → Exercises (31-42)

Click here for → Exercise(43-54)

CHAPTER- 7 - Circular Motion

Click here for → Questions for Short Answer 

Click here for → OBJECTIVE-I

Click here for → OBJECTIVE-II

Click here for → EXERCISES (1-10)

Click here for → EXERCISES (11-20)

Click here for → EXERCISES (21-30)

CHAPTER- 6 - Friction

Click here for → Questions for Short Answer

Click here for → OBJECTIVE-I

Click here for → Friction - OBJECTIVE-II

Click here for → EXERCISES (1-10)

Click here for → Exercises (11-20)

Click here for → EXERCISES (21-31)

For more practice on problems on friction solve these- "New Questions on Friction".

---------------------------------------------------------------------------------

CHAPTER- 5 - Newton's Laws of Motion

Click here for → QUESTIONS FOR SHORT ANSWER

Click here for→ Newton's laws of motion - Objective - I

Click here for → Newton's Laws of Motion - Objective -II

Click here for → Newton's Laws of Motion-Exercises(Q. No. 1 to 12)

Click here for→Newton's Laws of Motion,Exercises(Q.No. 13 to 27)

Click here for→Newton's Laws of Motion,Exercises(Q.No. 28 to 42)

-------------------------------------------------------------------------------

CHAPTER- 4 - The Forces

The Forces-

"Questions for short Answers"    

Click here for "The Forces" - OBJECTIVE-I

Click here for "The Forces" - OBJECTIVE-II

Click here for "The Forces" - Exercises

--------------------------------------------------------------------------------------------------------------

CHAPTER- 3 - Kinematics - Rest and Motion

Click here for "Questions for short Answers"

Click here for "OBJECTIVE-I"

Click here for EXERCISES (Question number 1 to 10)

Click here for EXERCISES (Question number 11 to 20)

Click here for EXERCISES (Question number 21 to 30)

Click here for EXERCISES (Question number 31 to 40)

Click here for EXERCISES (Question number 41 to 52)

CHAPTER- 2 - "Vector related Problems"

Click here for "Questions for Short Answers"

Click here for "OBJECTIVE-I

Click here for "OBJECTIVE-II"

Click here for "Exercises"