KKMishra's Tutorials: Solutions to Problems on "Work and Energy" - H C Verma's Concepts of Physics, Part-I, Chapter-8, EXERCISES Q-43 TO Q-54

My Channel on YouTube → SimplePhysics with KK

For links to

other chapters - See bottom of the page

WORK AND ENERGY:--
EXERCISES (43-54)

43. Figure (8-E7) shows a spring fixed at the bottom end of an incline of inclination 37°. A small block of mass 2.0 kg starts slipping down the incline from a point 4.8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find (a) the friction coefficient between the plane and the block and (b) the spring constant of the spring. Take g = 10 m/s².

Figure for Q-43

Answer: Let us draw a free body diagram of the block as below,

FBD of the block

(a) Forces on the block are weight mg, the force of friction F and normal force on the block N.

Equating the forces perpendicular to the plane,

N = mg.cos37°

Resolving all the forces along the plane we get net force

=mg.sin37°-µN =mg.sin37°-µ.mg.cos37°

Distance covered along the plane =4.8 m+ 0.20 m = 5.0 m

So, work done by all the forces on the block = Force x Distance

= (mg.sin37°- µ.mg.cos37°)x5.0 J ---------- (i)

This work done is stored as potential energy in the spring compression = ½kx² (where k=spring constant and x=compression of spring)

=½k(0.20)² J ------------------------------------- (ii)

When the block rebounds this stored P.E. is utilized in the movement of the block. In the return journey, the magnitude of the friction force remains the same but it's direction changes because it resists the movement. Now forces along the plane are = mg.sin37°+F =mg.sin37°+µ.mg.cos37°

Now it moves to a distance of 1.0 m

So, work done by the forces = Force x distance

= (mg.sin37°+µ.mg.cos37°)x1.0

=mg.sin37°+µ.mg.cos37° J --------------------- (iii)

All (i), (ii) and (iii) are equal. Equating (i) and (iii)

mg.sin37°+µ.mg.cos37° = (mg.sin37°- µ.mg.cos37°)x5.0

→µ.6mg.cos37° = 4mg.sin37°

→µ = 2tan37°/3 =2*0.75/3 =0.50

(b) Equating (ii) and (iii) we get,

½kx² = mg.sin37°+µ.mg.cos37°

k.(0.20)² = 2mg(sin37°+µ.cos37°)

→k = 2*2*10*(0.60+0.50*0.80)/0.04

→k=40*100*1.0/4 = 1000 N/m

44. A block of mass m moving at a speed v Compresses a spring through a distance x before its speed is halved. Find the spring constant of the spring.

Answer: Initial Kinetic Energy of the bock =½mv². This energy will be conserved even after the spring compression. Total energy at the point after spring compression of x =K.E. of the block + P.E. stored in the spring = ½m(v/2)²+½kx². (where k is the spring constant)

Equating initial and final energies we get,
½m(v/2)²+½kx²=½mv²
→mv²/4+kx²=mv²
→kx²=3mv²/4
→k=3mv²/4x²

45. Consider the situation shown in figure (8-E8). Initially, the spring is unstretched when the system is released from rest. Assuming no friction in the pulley, Find the maximum elongation of the spring.

Figure for Q 45

Answer: Let the maximum elongation of the spring be x. The block will also descend to x distance. So the reduction in P.E. of the block will be the P.E. stored in the spring.

Change in P.E. of the block = mg*x =mgx

P.E. stored in the spring = ½kx²

Equating these two,

½kx²=mgx

→x=2mg/k

46. A block of mass m is attached to two unstretched springs of spring constant k₁ and k₂ as shown in figure (8-E9). The block is displaced towards right through a distance of x and released. Find the speed of the block as it passes through the mean position shown.

Figure for Q 46

Answer: Let the speed of the block be v at the mean position. At the compressed position total energy is the P.E. stored in both the springs. i.e. equal to ½k₁x²+½k₂x²

At the mean position, this P.E. will be changed to K.E. of the block. i.e. equal to ½mv².

Equating both we get

½mv²=½k₁x²+½k₂x²

→mv²=k₁x²+k₂x²

→v²=(k₁+k₂)x²/m

→v=√{(k₁+k₂)/m}*x

47. A block of mass m sliding on a smooth horizontal surface with a velocity v meets a long horizontal spring fixed at one end and having spring constant k as shown in the figure (8-E10). Find the maximum compression of the spring. Will the velocity of the block be the same as v when it comes back to the original position shown?

Figure for Q 47

Answer: Initial K.E. of the block =½mv²

At the maximum Compression x, this K.E. will be changed to P.E. in the spring. This P.E. = ½kx²

Equating we get,

½kx²=½mv²

→kx²=mv²

→x²=mv²/k

→x=v√(m/k)

When it comes back to the original position its K.E. will again be the same (Assuming that there is no energy loss in the spring). Though the magnitude of the velocity of the block will be the same its direction will be opposite. Since velocity is a vector hence it is not the same as the original.

48. A small block of mass 100 g is pressed against a horizontal spring fixed at one end to compress the spring through 5.0 cm (Figure 8-E11). The spring constant is 100 N/m. When released, the block moves horizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?

Figure for Q 48

Answer: Mass of the block m=100 g =0.10 kg, Spring constant k = 100 N/m, Compression of the spring x= 5 cm = 0.05 m

P.E. stored in the spring = ½kx² =½*100*(0.05)² =0.125 J
This P.E. is converted as K.E. of the block when it leaves the spring =½mv²
i.e. ½mv²=0.125
→v²=0.25/m =0.25/0.10 =2.5
→v=√2.5 m/s
Let time taken to fall 2 m be t. In vertical direction u=0, h=2 m
from h=ut+½gt²
2 = 0+½*9.8t² =4.9t²
→t²=2/4.9
→t=√(2/4.9) s
In this time the block will move horizontally with a uniform velocity of v=√2.5 m/s
So the horizontal distance traveled = vt =√2.5*(√2/4.9) m
=√5/4.9 ≈1 m
So the block will hit the ground at a distance of 1 m from the free end of the spring.

49. A small heavy block is attached to the lower end of a light rod of length l which can be rotated about its clamped upper end. What minimum horizontal velocity should the block be given so that it moves in a complete vertical circle.

Answer: Let us take P.E. of the block at the lowest position be zero. If the velocity given be v, Then K.E. = ½mv²
So total energy at this level = P.E+K.E = ½mv²
If the velocity at the highest position is v', K.E. =½mv'² and P.E.=mg*2l =2mgl
Total energy =½mv'²+2mgl
Due to the conservation of energy, it will be same at both points. hence,
½mv²=½mv'²+2mgl
→v² = v'²+4gl
→v = √(v'²+4gl)
Since l and g are constants here, for v to be minimum v'² should be minimum, i.e. v'=0. Putting it in above expression we get,
v = √(0+4gl) =√4gl =2√(gl)

50. Figure (8-E12) shows two blocks A and B, each having a mass of 320 g connected by a light string passing over a smooth and light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to a spring of spring constant 40 N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g = 10 m/s².

Figure for Q 50

Answer: Let the spring make an angle θ with the horizontal at the instance it breaks off the surface and the force due to spring T. If the velocity at this instant is v, then total K.E. of the system =2*½mv² =mv².

K.E. at initial position = 0

Change in K.E. =mv²

Figure for Q 50

Given spring constant k=40N/m and Natural length of the spring h = 40 cm =0.40 m

Elongation of the spring x = h.cosecθ-h

Hence T=kx =k.(h.cosecθ-h)

Equating vertical forces on the block on the horizontal surface,

T.sinθ=mg →T=mg/sinθ

so, k.(h.cosecθ-h)=mg/sinθ

cosecθ-1=mg/khsinθ

1-sinθ=mg/kh

sinθ=1-mg/kh =1-0.32*10/40*0.4 =1-3.2/16 =12.8/16 = 0.8

Elongation x = h.cosecθ-h =0.4/0.8-0.4 =0.5-0.4 =0.1 m

Displacement s =h.cotθ =0.4*3/4 =0.3 m (Since cosθ=√(1-sin²θ) =√(1-0.8²) =√0.36 =0.6 and Cotθ = Cosθ/sinθ = 0.6/0.8 =3/4)

W.D. by all the forces on the system equals the change in K.E., so

-½kx²+mgs =mv² (negative sign is due to the elongation opposite to the force)

→v²=gs-½kx²/m =10*0.3-½*40*0.1²/0.32 (Given m=320 g =0.32 kg)
→v²=3-20*0.01/0.32 =3-0.20/0.32 =3-0.63 =2.37
→v = 1.53 m/s

51. One end of a spring of natural length h and spring constant k is fixed at the ground and the other is fitted with a smooth ring of mass m which is allowed to slide on a horizontal rod fixed at a height h (Figure 8-E13). Initially, the spring makes an angle of 37° with the vertical when the system is released from the rest. Find the speed of the ring when the spring becomes vertical.

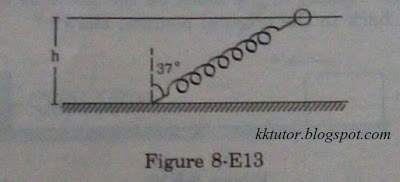Figure for Q 51

Answer: When the spring is at the given initial position its length =h*sec37°

Elongation from natural length = h.sec37°-h =1.25h-h =0.25h

P.E. stored in the spring = ½k(0.25h)²

When the spring comes in the vertical position, it retains its natural length and P.E. stored in it becomes zero but the ring which was at rest initially having its K.E. zero now has a kinetic energy due to its speed v at the final position. Since mechanical energy of the system will be conserved it means total P.E. of the spring is converted to K.E. of the ring =½mv²

Equating the two we get,

½mv² = ½k(0.25h)²

→mv² = k(0.25h)²

→v =0.25h√(k/m) = ¼h√(k/m)

52. Figure (8-E14) shows a light rod of length l rigidly attached to a small heavy block at one end and a hook at the other end. The system is released from rest with the rod in a horizontal position. There is a fixed smooth ring at a depth h below the initial position of the hook and the hook gets into the ring as it reaches there. What should be the minimum value of h so that the block moves in a complete circle about the ring?

Figure for Q 52

Answer: Since the rod is rigidly attached to the block hence when it makes a complete circle its height above the ring at the highest point will be equal to l. If its speed at the highest point is v then its total energy here is equal to K.E.+P.E =½mv²+mgl. This total energy is due to the P.E. of the block at height h = mgh (taking the ring as the zero P.E. level).

Equating the two we have,

mgh = ½mv²+mgl

→h = ½v²/g+l

Since l is fixed, for h to be minimum the first term ½v²/g should be minimum. It will be minimum when v=0. Putting this value in the expression we have,

h = 0 + l

→h = l

53. The bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √(10gl) where l is the length of the pendulum. Find the tension in the string when (a) the string is horizontal, (b) the bob is at its highest point and (c) the string makes an angle of 60° with the upward vertical.

Answer: Let us consider the position of the bob when the string makes an angle θ with the upward horizontal. See figure below,

Figure for Q 53

Let tension in the string be T, the mass of the bob = m, velocity = v.
Total centripetal force = T+mg.cosθ
Since its velocity is v, centripetal acceleration = v²/l
Since Force = mass x acceleration
T+mg.cosθ= mv²/l
→T = m(v²/l-g.cosθ) =m(v²-lg.cosθ)/l---------- (i)
Let us take bob at rest as base for P.E. i.e. P.E. = 0
Velocity given at this point = √10gl
K.E. = ½m*10gl
Total Energy = P.E.+K.E. = 5mgl -----(ii)
Now K.E. at present level = ½mv²
P.E. at present level = mg(l+l.cosθ) = mgl(1+cosθ)
Total Energy = ½mv²+mg1(1+cosθ) ----- (iii)
Total energy will be conserved, hence equating (ii) and (iii) we get,
½mv²+mg1(1+cosθ) = 5mgl
→mv²+2mgl(1+cosθ) = 10mgl
→mv² = 10mgl-2mgl(1+cosθ)=mgl(8-2.cosθ)
→v² = gl(8-2.cosθ)
Putting this in (i)
T = m(v²-lg.cosθ)/l =m{gl(8-2.cosθ)-lg.cosθ)}/l
=m{8gl-2gl.cosθ-gl.cosθ}/l = m(8g-3g.cosθ)

(a) When the string is horizontal, θ=90°
T = m(8g-3g.cos90°) =m(8g-3g*0) =8mg

(b) When the bob is at its highest point. θ = 0°
T= m(8g-3g.cos0°) =m(8g-3g) =m*5g =5mg

(c) When the string makes an angle 60° with the upward vertical, θ=60°
T = m(8g-3g.cos60°) = m(8g-3g*½) =m(8g-1.5g) =m*6.5g =6.5mg

54. A simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes an angle of 37° with the vertical and is then released. Find the tension in the string when the bob is at its lowest position.

Answer: Let us draw a figure as below,

Figure for Q 54

Length of the string OA = 50 cm = r (radius)
When the string makes an angle 37° with the vertical, the ball's height above its lowest position h= OB-OC =50-50*COS37° =50(1-4/5) =10 cm =0.10 m
Mass of the ball m =100 g =0.10 kg
Taking the ball's lowest position as base, P.E. given to the ball =mgh --------------------------- (i)
At the lowest position P.E. = 0 and K.E. =½mv², (where v= velocity)
Total Energy = ½mv² ------------------ (ii)
Total energy is conserved hence (i) and (ii) will be equal.
→½mv² = mgh
→v²=2gh
Let the tension in the string at its lowest position be T. Centripetal forces at this position = T-mg
Centripetal acceleration = v²/r
Hence T-mg=mv²/r

→T = mg+mv²/r
=mg+m*2gh/r
=mg(1+2h/r)
=0.10*9.8(1+2*0.10/0.50)
=0.98*(1+2/5)
=0.98*7/5
=1.372 N
≈1.4 N

===<<<O>>>===