My Channel on YouTube → SimplePhysics with KK
For links to
other chapters - See bottom of the page
Or click here → kktutor.blogspot.com
ROTATIONAL MECHANICS:--
EXERCISES-(Q61 to Q75)
61. Suppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. (a) Find the velocity of the center of mass C of the system constituting "the rod plus the particle". (b) Find the velocity of the particle with respect to C before the collision. (c) Find the velocity of the rod with respect to C before the collision. (d) Find the angular momentum of the particle and of the rod about the center of mass C before the collision. (e) Find the moment of inertia of the system about the vertical axis through the center of the mass C after the collision. (f) Find the velocity of the center of mass C and the angular velocity of the system about the center of mass after the collision.
ANSWER: (a) Let the velocity of the CoM of the system be v'.
The linear momentum will be conserved. so,
(m+M)v' = mv
→v' = mv/(m+M)
(b) The velocity of the particle w.r.t. CoM
v"= v - v'
= v - mv/(m+M)
= (mv+Mv-mv)/(m+M)
= Mv/(m+M)
(c) Let the velocity of the rod w.r.t C before collision = V
V = Velocity of the rod - velocity of CoM
= 0-v'
= -mv/(m+M)
(d) Let the distance of the C from the particle before the collision =x
x = (m*0+M*L/2)/(m+M)
=ML/2(m+M)
The angular momentum of the particle about c = mv"*ML/2(m+M)
=m*Mv/(m+M)*ML/2(m+M)
=mM²vL/2(m+M)²
(Anticlockwise)
The distance of C from the center of the rod, y = (L/2)-x
=(L/2)-ML/2(m+M)
=(mL+ML-ML)/2(m+M)
=mL/2(m+M)
The angular momentum of the rod about C = MV*mL/2(m+M)
=M*mv/(m+M)*mL/2(m+M)
=Mm²vL/2(m+M)²
(Anticlockwise)
(e) The moment of inertia of the system about C after the collision
= M.I. of the particle about C + M.I. of the rod about C
= mx² + ML²/12 + My²
= mM²L²/4(m+M)² +ML²/12 + Mm²L²/4(m+M)²
= {3mML²(M+m)+ML²(m+M)²}/12(m+M)²
={ML²(M+m)(3m+m+M)}/12(m+M)²
=ML²(4m+M)/12(m+M)
(f) The velocity of the CoM of the rod plus the particle has been calculated in (a) = mv/(M+m). It can also be calculated by finding the velocity of the CoM of the system just before the collision because there is no external force on the system so the velocity of the center of mass before the collision will be the same as after the collision.
The velocity of CoM before the collision = (M*0+mv)/(M+m)
=mv/(M+m)
The angular momentum will also be conserved. The angular momentum after the collision = the angular momentum before the collision
= The angular momentum of the particle about C + The angular momentum of the rod about C
= mM²vL/2(m+M)²+Mm²vL/2(m+M)²
[As calculated in (d)]
= mMvL(M+m)/2(M+m)²
= mMvL/2(M+m)
Let the angular speed of the rod be ⍵.
Then ⍵ = Angular Momentum/M.I
= {mMvL/2(M+m)}/{ML²(4m+M)/12(m+M)}
[M.I. of the system calculated in (e)]
=6mv/{L(4m+M)}
62. Two small balls A and B, each of mass m, are joined rigidly by a light horizontal rod of length L. The rod is clamped at the center in such a way that it can rotate freely about a vertical axis through its center. The system is rotated with an angular speed ⍵ about the axis. A particle P of mass m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
ANSWER: The moment of inertia of the ball system, I= 2*m(L/2)² = 2mL²/4 =mL²/2
The angular momentum of the system = I⍵ =mL²⍵/2
When the particle P of mass m sticks to the ball A the moment of inertia of the system changes.
The new moment of inertia I' = I+m(L/2)² =mL²/2+mL²/4 = 3mL²/4
Let the new angular speed be ⍵'
Since the angular momentum will be conserved, hence
I'⍵' =I⍵
→(3mL²/4)*⍵' = (mL²/2)*⍵
→3⍵'/4 = ⍵/2
→⍵' = 2⍵/3
63. Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (figure 10E-10). The system translates on a frictionless horizontal surface with a velocity v₀ in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the center of mass C of the system A+B+P and (c) the angular speed of the system about C after the collision.
[Hint: The light rod will exert a force on the ball B only along its length]
ANSWER: (a) Let the velocity of A after the strike = v'
Since the light rod will exert a force only along its length, the strike with the particle A will not affect the velocity of B. So
Equating the momentum of A before and after the collision.
mv₀ = 2mv'
→v' = v₀/2 (Velocity of A after the collision)
The velocity of B = v₀
(b) The velocity of the center of mass A+B+P = V
3mV = (2m*v₀/2+m*v₀)
→3mV = 2mv₀
→V = 2v₀/3
{Along the initial direction of the velocities.}
(c)Let the angular speed of the system about C be ⍵.
The distance of CoM from A = x = mL/3m =L/3
and from B = 2L/3.
Let us consider the velocities of A and B with respect to CoM.
The velocity of A w,r,t CoM = v₀/2 -2v₀/3
= (3v₀-4v₀)/6
= -v₀/6 {negative sign says the velocity of A is towards left with respect to CoM}
Hence, ⍵ = Velocity/radius = (v₀/6)/(L/3) = (v₀/6)*(3/L)
= v₀/2L (Clockwise).
It can be confirmed with respect to particle B also. Velocity of B w.r.t. CoM = v₀ -2v₀/3 =v₀/3 {Towards right}
Hence ⍵ = (v₀/3)/(2L/3) =(v₀/3)*(3/2L) = v₀/2L (Clockwise)
64. The rod with the balls A and B of the previous problem are clamped at the center in such a way that it rotates freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a height h on the ball B. The particle collides with B and sticks to it. (a) Find the angular momentum and the angular speed of the system just after the collision. (b) what should be the minimum value of h so that the system makes a full rotation after the collision.
ANSWER: (a) The speed of the particle P when it reaches ball B = v = √(2gh)
Hence the angular momentum of the particle P about the horizontal axis (center of the rod) = mass*velocity*radius
= m*√(2gh)*L/2
= mL√(gh)/√2
Since there is no external force on the system, this angular momentum will be conserved even after the strike.
Let the angular speed of the rod after the strike be ⍵. Now the moment of inertia I about the center = 2m(L/2)²+m(L/2)²
=3mL²/4
The angular momentum = I⍵ =3mL²⍵/4
Equating this with the angular momentum calculated above, we get
3mL²⍵/4 = mL√(gh)/√2
→⍵ = (4/3L)*√(gh)/√2
= 4√2√(gh)/6L {Multiplying num. and den. by √2}
=2√2√(gh)/3L
=√(8gh)/3L
(b) The kinetic energy after the strike =½I⍵²
=½*3mL²/4*{√8gh)/3L}²
=(3mL²/8)*8gh/9L²
=mgh/3
Let us take the horizontal axis as a reference for P.E. The system will just complete a full rotation if the ball B with particle P just reaches the topmost position. Here the K.E. will be zero and fully converted to P.E. At this position the P.E. = 2mg*L/2-mg*L/2
= mgL/2
Equating K.E. and P.E.
mgh/3 = mgL/2
→h/3 = L/2
→h = 3L/2
65. Two blocks of masses 400g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia 1.6x10⁻⁴ kg-m² and a radius 2.0 cm. Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
ANSWER: (a) M = 400 g = 0.40 kg
m = 200 g = 0.20 kg
the fall of mass 400 g = h = 50 cm =0.50 m
Drop in P.E. of the 400 g = mgh = 0.40*9.8*0.50 J
= 1.96 J
Simultaneously the 200 g mass will rise through 0.50 m, hence rise in P.E. of 200 g
=0.20*9.8*0.50 J = 0.98 J
Net loss of P.E. = 1.96 - 0.98 = 0.98 J
Hence eaqual amout will convert to K.E. = 0.98 J
(b) I = 1.6x10⁻⁴ kg-m², r = 2.0 cm = 0.02 m
Let the speed of the blocks at this instant be = v
The angular speed of the pulley = ⍵ = v/r
Total K.E. of the system = K.E. of the 400 g mass + K.E. of the 200 g mass + K.E. of the pulley
= ½*0.40*v²+½*0.20*v²+½I⍵²
=0.20v²+0.10v²+½* 1.6x10⁻⁴ (v/0.02)²
=0.30v²+ 1.6x10⁻⁴ v²/0.0008 J
=0.30v²+1.6v²/8 J
=0.30v²+0.20v² =0.50v² J
But it has been calculated to be 0.98 J in part (a) of the problem. Equating,
0.50v² = 0.98
→v² = 0.98/0.50 =1.96
→v = 1.4 m/s
66. The pulley shown in the figure (10E-11) has a radius of 20 cm and a moment of inertia 0.20 kg-m². The string going over it is attached at one end to a vertical spring of spring constant 50 N/m fixed from below and supports a 1 kg mass at the other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has descended through 10 cm. Take g = 10 m/s².
ANSWER: Let the speed of the block be v when it descends through 10 cm. At this time the spring is also stretched through 10 cm. So the force on the spring = kx = 50*10/100 = 5 N
So the P.E. stored in the spring =½kx² = 0.5*50*0.10*0.10
=25*0.01 =0.25 J
Radius of the pulley, r = 20 cm = 0.20 m.
Moment of inertia of the pulley = I = 0.20 kg-m².
The angular speed of the pulley, ⍵ =v/r = v/0.20
K.E. of the pulley = ½I⍵² =½*0.20*v²/(0.20)² =v²/0.4
K.E. of the block = ½mv² =0.50*1*v² = 0.50 v² J
Loss of P.E. of the block = mgh = 1*10*0.10 = 1 J
Loss of P.E. of the block = Energy stored in the spring + K.E. of the pulley + K.E. of the block
1 = 0.25+ v²/0.4 +0.50v²
→2.5 v² + 0.50 v² = 0.75
→3 v² = 0.75
→v² = 0.25
→v = 0.50 m/s
67. A meter stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
ANSWER: The height of the center of mass of the stick from the floor = 0.50 m
P.E. of the stick in the vertical position = mgh = 0.50mg J
When it hits the floor its P.E. becomes zero and it is converted to K.E. Let the angular speed of the stick when it hits the ground = ⍵
K.E. of the stick = ½I⍵²
Since the stick rotates about the end, the M.I. about the end
= I₀+mr²
= ml²/12 + m(l/2)²
=ml²/12 + ml²/4
=4ml²/12
=ml²/3
Now K.E. of the stick = ½*ml²⍵²/3 J
= ml²⍵²/6 J
K.E. = P.E.
ml²⍵²/6 = 0.50mg
⍵² = 3g/l² = 3*9.8 rad/s [l = 1 m]
= 29.4
⍵ = 5.4 rad/s
68. A meter stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end (figure 10E-12). A particle of mass 100 g is attached to the upper end of the stick through a light string of length 1 m. Initially, the rod is kept vertical and the string horizontal when the system is released from the rest. The particle collides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.
ANSWER: Mass of the stick M = 240 g =0.24 kg
Mass of the particle m = 100 g =0.10 kg
Let the angular speed of the particle with string = ⍵
M.I. = I = ml² = 0.10*1² =0.10 kg-m²
The rotational energy of the string particle =P.E.
→½I⍵²=mgl
→0.5*0.10*⍵² = 0.10g*1
→⍵² =g/0.5 =2g
→⍵=√(2g)
The angular momentum of the system before the strike
= Angular momentum of the string-particle+Angular momentum of the rod
=I⍵+0=I⍵
=0.10⍵ =0.10√2g
Let the angular speed of the rod after the strike be ⍵'
Now the angular momentum = I'⍵'
=(Ml²/3+ml²)⍵'
=(0.24/3+0.10)⍵'
=0.18⍵'
The angular momentum will be conserved.
→0.18⍵' = 0.10√(2g)
→⍵' = 10√2√g/18 =0.786√g
KE =½I'⍵'² =0.5*0.18*⍵'² =0.09*0.786*0.786g=0.055 g ...(i)
the change in PE of the system at angle θ after the strike
= mg(1-cosθ)+Mg(½-½cosθ)
=0.10g(1-cosθ)+0.12g(1-cosθ)
=(1-cosθ)*0.22g ....................(ii)
Equating (i) and (ii)
(1-cosθ)*0.22g = 0.055g
→1-cosθ = 0.055/0.22 = 0.252
→cosθ = 1-0.252 = 0.747
→θ ≈ 41°
69. A uniform rod pivoted at its upper end hangs vertically. It is displaced through an angle of 60° and then released. Find the magnitude of the force acting on a particle of mass dm at the tip of the rod when the rod makes an angle of 37° with the vertical.
ANSWER: Let the mass of the rod be m and length l. If the angular speed of the rod at 37° be ⍵, then change in K.E. of the rod should be equal to change in P.E. of the rod.
Change in K.E. = ½I⍵² - 0 = ½*ml²/3*⍵² =ml²⍵²/6
Change in P.E. = mg(vertical distance of the center of the rod at 37°-vertical distance of the center of the rod at 60°)
=mg(½l.cos37°-½l.cos60°)
=½mgl(cos37°-cos60°)
=½mgl(0.80-0.5)
=½mgl*0.3 =0.3mgl/2
Equating we get,
ml²⍵²/6 = 0.3mgl/2
→⍵² = 0.9g/l
Let the angular acceleration at 37° be α. Equating the torque at this point,
Iα =mg.sin37°*½l
{mg.sin37° is the component of the weight of the rod perpendicular to it and acting at the center of the rod. Multiplying it by l/2 we get the torque about the pivot}
→ml²/3*α = ½*0.60*mgl =0.30mgl
→α = (3/l)*0.30g =0.90g/l
There will be tangential and radial forces on the particle dm at the tip of the rod.
Radial force Fₓ = dm*⍵²l =dm*(0.9g/l)*l =0.9dm g
Tangential force Fᵧ = mass*acceleration = dm*αl =dm*l*0.90g/l =0.9dm g = Fₓ
These two forces are perpendicular to each other.
Hence the resultant force on the particle dm, F =√(Fₓ²+Fᵧ²) =√2Fₓ
=√2*0.90dm.g
=0.9√2dm.g
70. A cylinder rolls on a horizontal plane surface. If the speed of the center is 25 m/s, what is the speed of the highest point?
ANSWER: When a cylinder or wheel rolls on a surface the speed of the point in contact is zero and its vertical diameter can be considered as rotating about the point of contact. Let the angular speed of the vertical diameter about the point of contact be ⍵.
⍵ = v/r =25/r rad/s. If the speed of the highest point be V, then
V = ⍵*2r =(25/r)*2r =50 m/s
71. A sphere of mass m rolls on a plane surface. Find its kinetic energy at an instant when its center moves with speed v.
ANSWER: At this stage, the sphere will have linear as well as rotational kinetic energy.
K.E. = ½mv² + ½I⍵²
I = 2mr²/5
⍵ = v/r
Hence total K.E. = ½mv²+½*(2mr²/5)*v²/r²
=½mv²+mv²/5
=7mv²/10
72. A string is wrapped over the edge of a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
ANSWER: Let the acceleration of the disc be a and the tension in the string T. If the radius of the disc is r, then torque on the disc = Tr.
Now, mg - T = ma
→T =mg-ma
The angular acceleration of the disc = α = a/r
Torque = Iα
Tr = ½mr²*a/r
→2T = ma
→2mg-2ma = ma
→2g =3a
→a = 2g/3
73. A small spherical ball is released from a point at a height h on a rough track shown in figure (10-E13). Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.
ANSWER: The P.E. of the ball = mgh will be converted to K.E. of the ball when it rolls on the horizontal part of the track.
Let the linear speed of the ball be v. Translational K.E. = ½mv²
The angular speed of the ball ⍵ = v/r
and the moment of inertia of the ball, I =2mr²/5
The angular K.E. = ½I⍵² = ½*2mr²/5*⍵² = mr²⍵²/5
Equating the total K.E. and the P.E.
½mv² + mr²⍵²/5 = mgh
→5v²+2r²(v/r)² = 10gh
→7v² = 10gh
→v² = 10gh/7
→v = √(10gh/7)
74. A small disc is set rolling with a speed v on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
ANSWER: Let the required height be h.
M.I. of the disc, I =½mr²
The angular speed ⍵ = v/r
The rotational K.E. =½I⍵² = ½*½mr²*v²/r² = ¼mv²
Translational K.E. = ½mv²
Total K.E. on the horizontal part = ¼mv² + ½mv² = ¾mv²
This total K.E. will be converted to P.E. at maximum height h = mgh. Equating,
mgh = ¾mv²
→h = ¾v²/g
75. A sphere starts rolling down an incline of inclination 𝛉, find the speed of its center when it has covered a distance l.
ANSWER: When the sphere covers a distance of l on the incline it descends through a height l.sinθ. Loss of its P.E. =mgl.sinθ
Let the speed of its center be v and the angular speed ⍵ at the given position.
Linear K.E. =½mv²
Rotational K.E. =½I⍵² = ½*2mr²/5*v²/r² =mv²/5
Total K.E. = ½mv² + mv²/5
=7mv²/10
Equating we get,
7mv²/10 = mgl.sinθ
→v² = 10gl.sinθ/7
→v = √(10gl.sinθ/7)
ANSWER: (a) Let the velocity of the CoM of the system be v'.
The linear momentum will be conserved. so,
(m+M)v' = mv
→v' = mv/(m+M)
(b) The velocity of the particle w.r.t. CoM
v"= v - v'
= v - mv/(m+M)
= (
= Mv/(m+M)
(c) Let the velocity of the rod w.r.t C before collision = V
V = Velocity of the rod - velocity of CoM
= 0-v'
= -mv/(m+M)
(d) Let the distance of the C from the particle before the collision =x
x = (m*0+M*L/2)/(m+M)
=ML/2(m+M)
The angular momentum of the particle about c = mv"*ML/2(m+M)
=m*Mv/(m+M)*ML/2(m+M)
=mM²vL/2(m+M)²
(Anticlockwise)
The distance of C from the center of the rod, y = (L/2)-x
=(L/2)-ML/2(m+M)
=(mL+ML-ML)/2(m+M)
=mL/2(m+M)
The angular momentum of the rod about C = MV*mL/2(m+M)
=M*mv/(m+M)*mL/2(m+M)
=Mm²vL/2(m+M)²
(Anticlockwise)
(e) The moment of inertia of the system about C after the collision
= M.I. of the particle about C + M.I. of the rod about C
= mx² + ML²/12 + My²
= mM²L²/4(m+M)² +ML²/12 + Mm²L²/4(m+M)²
= {3mML²(M+m)+ML²(m+M)²}/12(m+M)²
={ML²(M+m)(3m+m+M)}/12(m+M)²
=ML²(4m+M)/12(m+M)
(f) The velocity of the CoM of the rod plus the particle has been calculated in (a) = mv/(M+m). It can also be calculated by finding the velocity of the CoM of the system just before the collision because there is no external force on the system so the velocity of the center of mass before the collision will be the same as after the collision.
The velocity of CoM before the collision = (M*0+mv)/(M+m)
=mv/(M+m)
The angular momentum will also be conserved. The angular momentum after the collision = the angular momentum before the collision
= The angular momentum of the particle about C + The angular momentum of the rod about C
= mM²vL/2(m+M)²+Mm²vL/2(m+M)²
[As calculated in (d)]
= mMvL(M+m)/2(M+m)²
= mMvL/2(M+m)
Let the angular speed of the rod be ⍵.
Then ⍵ = Angular Momentum/M.I
= {mMvL/2(M+m)}/{ML²(4m+M)/12(m+M)}
[M.I. of the system calculated in (e)]
=6mv/{L(4m+M)}
62. Two small balls A and B, each of mass m, are joined rigidly by a light horizontal rod of length L. The rod is clamped at the center in such a way that it can rotate freely about a vertical axis through its center. The system is rotated with an angular speed ⍵ about the axis. A particle P of mass m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
ANSWER: The moment of inertia of the ball system, I= 2*m(L/2)² = 2mL²/4 =mL²/2
The angular momentum of the system = I⍵ =mL²⍵/2
When the particle P of mass m sticks to the ball A the moment of inertia of the system changes.
The new moment of inertia I' = I+m(L/2)² =mL²/2+mL²/4 = 3mL²/4
Let the new angular speed be ⍵'
Since the angular momentum will be conserved, hence
I'⍵' =I⍵
→(3mL²/4)*⍵' = (mL²/2)*⍵
→3⍵'/4 = ⍵/2
→⍵' = 2⍵/3
63. Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (figure 10E-10). The system translates on a frictionless horizontal surface with a velocity v₀ in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the center of mass C of the system A+B+P and (c) the angular speed of the system about C after the collision.
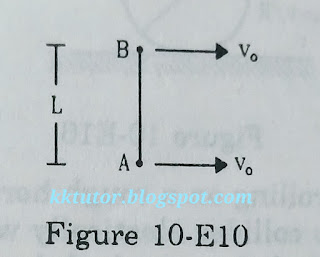 |
| Figure for Problem - 63 |
[Hint: The light rod will exert a force on the ball B only along its length]
ANSWER: (a) Let the velocity of A after the strike = v'
Since the light rod will exert a force only along its length, the strike with the particle A will not affect the velocity of B. So
Equating the momentum of A before and after the collision.
mv₀ = 2mv'
→v' = v₀/2 (Velocity of A after the collision)
The velocity of B = v₀
(b) The velocity of the center of mass A+B+P = V
3mV = (2m*v₀/2+m*v₀)
→3mV = 2mv₀
→V = 2v₀/3
{Along the initial direction of the velocities.}
(c)Let the angular speed of the system about C be ⍵.
The distance of CoM from A = x = mL/3m =L/3
and from B = 2L/3.
Let us consider the velocities of A and B with respect to CoM.
The velocity of A w,r,t CoM = v₀/2 -2v₀/3
= (3v₀-4v₀)/6
= -v₀/6 {negative sign says the velocity of A is towards left with respect to CoM}
Hence, ⍵ = Velocity/radius = (v₀/6)/(L/3) = (v₀/6)*(3/L)
= v₀/2L (Clockwise).
It can be confirmed with respect to particle B also. Velocity of B w.r.t. CoM = v₀ -2v₀/3 =v₀/3 {Towards right}
Hence ⍵ = (v₀/3)/(2L/3) =(v₀/3)*(3/2L) = v₀/2L (Clockwise)
64. The rod with the balls A and B of the previous problem are clamped at the center in such a way that it rotates freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a height h on the ball B. The particle collides with B and sticks to it. (a) Find the angular momentum and the angular speed of the system just after the collision. (b) what should be the minimum value of h so that the system makes a full rotation after the collision.
ANSWER: (a) The speed of the particle P when it reaches ball B = v = √(2gh)
Hence the angular momentum of the particle P about the horizontal axis (center of the rod) = mass*velocity*radius
= m*√(2gh)*L/2
= mL√(gh)/√2
Since there is no external force on the system, this angular momentum will be conserved even after the strike.
Let the angular speed of the rod after the strike be ⍵. Now the moment of inertia I about the center = 2m(L/2)²+m(L/2)²
=3mL²/4
The angular momentum = I⍵ =3mL²⍵/4
Equating this with the angular momentum calculated above, we get
3mL²⍵/4 = mL√(gh)/√2
→⍵ = (4/3L)*√(gh)/√2
= 4√2√(gh)/6L {Multiplying num. and den. by √2}
=2√2√(gh)/3L
=√(8gh)/3L
(b) The kinetic energy after the strike =½I⍵²
=½*3mL²/4*{√8gh)/3L}²
=(3mL²/8)*8gh/9L²
=mgh/3
Let us take the horizontal axis as a reference for P.E. The system will just complete a full rotation if the ball B with particle P just reaches the topmost position. Here the K.E. will be zero and fully converted to P.E. At this position the P.E. = 2mg*L/2-mg*L/2
= mgL/2
Equating K.E. and P.E.
mgh/3 = mgL/2
→h/3 = L/2
→h = 3L/2
65. Two blocks of masses 400g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia 1.6x10⁻⁴ kg-m² and a radius 2.0 cm. Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
ANSWER: (a) M = 400 g = 0.40 kg
m = 200 g = 0.20 kg
the fall of mass 400 g = h = 50 cm =0.50 m
Drop in P.E. of the 400 g = mgh = 0.40*9.8*0.50 J
= 1.96 J
Simultaneously the 200 g mass will rise through 0.50 m, hence rise in P.E. of 200 g
=0.20*9.8*0.50 J = 0.98 J
Net loss of P.E. = 1.96 - 0.98 = 0.98 J
Hence eaqual amout will convert to K.E. = 0.98 J
(b) I = 1.6x10⁻⁴ kg-m², r = 2.0 cm = 0.02 m
Let the speed of the blocks at this instant be = v
The angular speed of the pulley = ⍵ = v/r
Total K.E. of the system = K.E. of the 400 g mass + K.E. of the 200 g mass + K.E. of the pulley
= ½*0.40*v²+½*0.20*v²+½I⍵²
=0.20v²+0.10v²+½* 1.6x10⁻⁴ (v/0.02)²
=0.30v²+ 1.6x10⁻⁴ v²/0.0008 J
=0.30v²+1.6v²/8 J
=0.30v²+0.20v² =0.50v² J
But it has been calculated to be 0.98 J in part (a) of the problem. Equating,
0.50v² = 0.98
→v² = 0.98/0.50 =1.96
→v = 1.4 m/s
66. The pulley shown in the figure (10E-11) has a radius of 20 cm and a moment of inertia 0.20 kg-m². The string going over it is attached at one end to a vertical spring of spring constant 50 N/m fixed from below and supports a 1 kg mass at the other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has descended through 10 cm. Take g = 10 m/s².
 |
| The figure for problem 66 |
ANSWER: Let the speed of the block be v when it descends through 10 cm. At this time the spring is also stretched through 10 cm. So the force on the spring = kx = 50*10/100 = 5 N
So the P.E. stored in the spring =½kx² = 0.5*50*0.10*0.10
=25*0.01 =0.25 J
Radius of the pulley, r = 20 cm = 0.20 m.
Moment of inertia of the pulley = I = 0.20 kg-m².
The angular speed of the pulley, ⍵ =v/r = v/0.20
K.E. of the pulley = ½I⍵² =½*0.20*v²/(0.20)² =v²/0.4
K.E. of the block = ½mv² =0.50*1*v² = 0.50 v² J
Loss of P.E. of the block = mgh = 1*10*0.10 = 1 J
Loss of P.E. of the block = Energy stored in the spring + K.E. of the pulley + K.E. of the block
1 = 0.25+ v²/0.4 +0.50v²
→2.5 v² + 0.50 v² = 0.75
→3 v² = 0.75
→v² = 0.25
→v = 0.50 m/s
67. A meter stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
ANSWER: The height of the center of mass of the stick from the floor = 0.50 m
P.E. of the stick in the vertical position = mgh = 0.50mg J
When it hits the floor its P.E. becomes zero and it is converted to K.E. Let the angular speed of the stick when it hits the ground = ⍵
K.E. of the stick = ½I⍵²
Since the stick rotates about the end, the M.I. about the end
= I₀+mr²
= ml²/12 + m(l/2)²
=ml²/12 + ml²/4
=4ml²/12
=ml²/3
Now K.E. of the stick = ½*ml²⍵²/3 J
= ml²⍵²/6 J
K.E. = P.E.
ml²⍵²/6 = 0.50mg
⍵² = 3g/l² = 3*9.8 rad/s [l = 1 m]
= 29.4
⍵ = 5.4 rad/s
68. A meter stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end (figure 10E-12). A particle of mass 100 g is attached to the upper end of the stick through a light string of length 1 m. Initially, the rod is kept vertical and the string horizontal when the system is released from the rest. The particle collides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.
 |
| Figure for problem-68 |
ANSWER: Mass of the stick M = 240 g =0.24 kg
Mass of the particle m = 100 g =0.10 kg
Let the angular speed of the particle with string = ⍵
M.I. = I = ml² = 0.10*1² =0.10 kg-m²
The rotational energy of the string particle =P.E.
→½I⍵²=mgl
→0.5*0.10*⍵² = 0.10g*1
→⍵² =g/0.5 =2g
→⍵=√(2g)
The angular momentum of the system before the strike
= Angular momentum of the string-particle+Angular momentum of the rod
=I⍵+0=I⍵
=0.10⍵ =0.10√2g
Let the angular speed of the rod after the strike be ⍵'
Now the angular momentum = I'⍵'
=(Ml²/3+ml²)⍵'
=(0.24/3+0.10)⍵'
=0.18⍵'
The angular momentum will be conserved.
→0.18⍵' = 0.10√(2g)
→⍵' = 10√2√g/18 =0.786√g
KE =½I'⍵'² =0.5*0.18*⍵'² =0.09*0.786*0.786g=0.055 g ...(i)
the change in PE of the system at angle θ after the strike
= mg(1-cosθ)+Mg(½-½cosθ)
=0.10g(1-cosθ)+0.12g(1-cosθ)
=(1-cosθ)*0.22g ....................(ii)
Equating (i) and (ii)
(1-cosθ)*0.22g = 0.055g
→1-cosθ = 0.055/0.22 = 0.252
→cosθ = 1-0.252 = 0.747
→θ ≈ 41°
69. A uniform rod pivoted at its upper end hangs vertically. It is displaced through an angle of 60° and then released. Find the magnitude of the force acting on a particle of mass dm at the tip of the rod when the rod makes an angle of 37° with the vertical.
ANSWER: Let the mass of the rod be m and length l. If the angular speed of the rod at 37° be ⍵, then change in K.E. of the rod should be equal to change in P.E. of the rod.
 |
| Figure for Q-69 |
Change in K.E. = ½I⍵² - 0 = ½*ml²/3*⍵² =ml²⍵²/6
Change in P.E. = mg(vertical distance of the center of the rod at 37°-vertical distance of the center of the rod at 60°)
=mg(½l.cos37°-½l.cos60°)
=½mgl(cos37°-cos60°)
=½mgl(0.80-0.5)
=½mgl*0.3 =0.3mgl/2
Equating we get,
ml²⍵²/6 = 0.3mgl/2
→⍵² = 0.9g/l
Let the angular acceleration at 37° be α. Equating the torque at this point,
Iα =mg.sin37°*½l
{mg.sin37° is the component of the weight of the rod perpendicular to it and acting at the center of the rod. Multiplying it by l/2 we get the torque about the pivot}
→ml²/3*α = ½*0.60*mgl =0.30mgl
→α = (3/l)*0.30g =0.90g/l
There will be tangential and radial forces on the particle dm at the tip of the rod.
Radial force Fₓ = dm*⍵²l =dm*(0.9g/l)*l =0.9dm g
Tangential force Fᵧ = mass*acceleration = dm*αl =dm*l*0.90g/l =0.9dm g = Fₓ
These two forces are perpendicular to each other.
Hence the resultant force on the particle dm, F =√(Fₓ²+Fᵧ²) =√2Fₓ
=√2*0.90dm.g
=0.9√2dm.g
70. A cylinder rolls on a horizontal plane surface. If the speed of the center is 25 m/s, what is the speed of the highest point?
ANSWER: When a cylinder or wheel rolls on a surface the speed of the point in contact is zero and its vertical diameter can be considered as rotating about the point of contact. Let the angular speed of the vertical diameter about the point of contact be ⍵.
⍵ = v/r =25/r rad/s. If the speed of the highest point be V, then
V = ⍵*2r =(25/r)*2r =50 m/s
71. A sphere of mass m rolls on a plane surface. Find its kinetic energy at an instant when its center moves with speed v.
ANSWER: At this stage, the sphere will have linear as well as rotational kinetic energy.
K.E. = ½mv² + ½I⍵²
I = 2mr²/5
⍵ = v/r
Hence total K.E. = ½mv²+½*(2mr²/5)*v²/r²
=½mv²+mv²/5
=7mv²/10
72. A string is wrapped over the edge of a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
ANSWER: Let the acceleration of the disc be a and the tension in the string T. If the radius of the disc is r, then torque on the disc = Tr.
 |
| Figure for poblem - 72 |
Now, mg - T = ma
→T =mg-ma
The angular acceleration of the disc = α = a/r
Torque = Iα
Tr = ½mr²*a/r
→2T = ma
→2mg-2ma = ma
→2g =3a
→a = 2g/3
73. A small spherical ball is released from a point at a height h on a rough track shown in figure (10-E13). Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.
 |
| The figure for Problem - 73 |
Let the linear speed of the ball be v. Translational K.E. = ½mv²
The angular speed of the ball ⍵ = v/r
and the moment of inertia of the ball, I =2mr²/5
The angular K.E. = ½I⍵² = ½*2mr²/5*⍵² = mr²⍵²/5
Equating the total K.E. and the P.E.
½mv² + mr²⍵²/5 = mgh
→5v²+2r²(v/r)² = 10gh
→7v² = 10gh
→v² = 10gh/7
→v = √(10gh/7)
74. A small disc is set rolling with a speed v on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
ANSWER: Let the required height be h.
M.I. of the disc, I =½mr²
The angular speed ⍵ = v/r
The rotational K.E. =½I⍵² = ½*½mr²*v²/r² = ¼mv²
Translational K.E. = ½mv²
Total K.E. on the horizontal part = ¼mv² + ½mv² = ¾mv²
This total K.E. will be converted to P.E. at maximum height h = mgh. Equating,
mgh = ¾mv²
→h = ¾v²/g
75. A sphere starts rolling down an incline of inclination 𝛉, find the speed of its center when it has covered a distance l.
ANSWER: When the sphere covers a distance of l on the incline it descends through a height l.sinθ. Loss of its P.E. =mgl.sinθ
Let the speed of its center be v and the angular speed ⍵ at the given position.
Linear K.E. =½mv²
Rotational K.E. =½I⍵² = ½*2mr²/5*v²/r² =mv²/5
Total K.E. = ½mv² + mv²/5
=7mv²/10
Equating we get,
7mv²/10 = mgl.sinθ
→v² = 10gl.sinθ/7
→v = √(10gl.sinθ/7)
===<<<O>>>===
Links to the chapters -
ALL LINKS
CHAPTER- 10 - Rotational Mechanics
Questions for Short Answers
OBJECTIVE - I
OBJECTIVE - II
EXERCISES- Q-1 TO Q-15
EXERCISES- Q-16 TO Q-30
EXERCISES- Q-31 TO Q-45
EXERCISES- Q-46 TO Q-60
CHAPTER- 10 - Rotational Mechanics
Questions for Short Answers
OBJECTIVE - I
OBJECTIVE - II
EXERCISES- Q-1 TO Q-15
EXERCISES- Q-16 TO Q-30
EXERCISES- Q-31 TO Q-45
EXERCISES- Q-46 TO Q-60
CHAPTER- 9 - Center of Mass, Linear Momentum, Collision
HC Verma's Concepts of Physics, Chapter-8, WORK AND ENERGY
Click here for → Question for Short Answers
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → Exercises (1-10)
Click here for → Exercises (11-20)
Click here for → Exercises (21-30)
Click here for → Exercises (31-42)
Click here for → Exercise(43-54)
Click here for → Exercises (31-42)
Click here for → Exercise(43-54)
HC Verma's Concepts of Physics, Chapter-7, Circular Motion
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-30)
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-30)
HC Verma's Concepts of Physics, Chapter-6, Friction
Click here for → Friction OBJECTIVE-I
Click here for → Friction - OBJECTIVE-II
Click here for → Friction - OBJECTIVE-II
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
---------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-5, Newton's Law's of Motion
Click here for → QUESTIONS FOR SHORT ANSWER
Click here for→ Newton's laws of motion - Objective - I
Click here for → Newton's Laws of Motion - Objective -II
Click here for → Newton's Laws of Motion-Exercises(Q. No. 1 to 12)
Click here for→Newton's Laws of Motion,Exercises(Q.No. 13 to 27)
-------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-4, The Forces
"Questions for short Answers"
Click here for "The Forces" - OBJECTIVE-I
Click here for "The Forces" - OBJECTIVE-II
Click here for "The Forces" - Exercises
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------
Sir I want to first thank you for all the help you have been giving us.
ReplyDeleteKindly fix the mistake in question no.66 where you have written the equations. I believe you have missed out a (1/2)Iw^2 for which your answer does not turn out to be right.
Thank you.
Dear student, I have corrected it. Thank you for pointing the mistake.
Delete