My Channel on YouTube → SimplePhysics with KK
For links to
other chapters - See bottom of the page
Or click here → kktutor.blogspot.com
ROTATIONAL MECHANICS:--
EXERCISES-(Q76 to Q86)
76. A hollow Sphere is released from the top of an inclined plane of inclination θ. (a) What should be the minimum coefficient of friction between the sphere and the plane to prevent sliding? (b) Find the kinetic energy of the ball as it moves down a length l on the incline if the friction coefficient is half the value calculated in part (a).
ANSWER: Let the friction coefficient be µ. If the weight of the hollow sphere is m the normal force on it by the plane = mg.cosθ and hence the frictional force F = µmg.cosθ. The component of weight along the plane = mg.sinθ.
The torque on the ball due to frictional force about the point of contact = µmgr.cosθ {where r is the radius of the ball}
M.I. of the ball = 2mr²/3
(a) If the ball does not slide the angular acceleration of the ball,
α = µmgr.cosθ/2mr²/3
=3µg.cosθ/2r
With this angular acceleration the linear acceleration of the CoM (here the center of the sphere) a = αr = (3µg.cosθ/2r)*r =3µg.cosθ/2
If the sphere does not slide then the following condition should be satisfied
mg.sinθ-F =ma
mg.sinθ-µmg.cosθ =m3µg.cosθ/2
→sinθ = µ.cosθ+3µ.cosθ/2 =5µ.cosθ/2
→5µ.cosθ/2 = sinθ
→µ = 2.tanθ/5
(b) Now the frictional coefficient µ' =µ/2 = tanθ/5
Hence the frictional force F = µmg.cosθ
=mg.cosθ*tanθ/5
=mgsinθ/5
Torque on the ball = Fr=mgr.sinθ/5
α = Fr/I = (mgr.sinθ/5)/2mr²/3
=3g.sinθ/10r
Now mg.sinθ - F = ma
mg.sinθ - mg.sinθ/5 = ma
→a = 4g.sinθ/5
After moving distance l down the plane
v² = 0²+2al
→v = √(2al)
Also v = 0+at
→t = v/a =√(2al)/a =√(2l/a) =√(2l/4g.sinθ/5)
=√(5l/2g.sinθ)
And ⍵ = 0 +αt
=(3g.sinθ/10r)*√(5l/2g.sinθ)
=3{(5l)(g.sinθ)}1/2 /10r√2
The kinetic energy of the ball after it moves down a length l on the plane
=½mv²+½I⍵²
=½m*2al + ½*2mr²/3* 45l(g.sinθ)/(200r²)
=ml*4g.sinθ/5+45mlg.sinθ/600
=4mlg.sinθ/5 +3mlg.sinθ/40
={(32+3)/40}mlg.sinθ
=(35/40)mlg.sinθ
=(7/8)mlg.sinθ
77. A Solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
ANSWER: Here our aim is to first find the velocity of the ball when it reaches the bottom of the cup. If the radius of the hemispherical cup is R, then K.E. of the ball at the bottom
= the loss in P.E. = mg(R-r) {Where m is the mass of the ball and the CoM of the ball will be r above the bottom}
But it is also = ½mv²+½I⍵²
=½mv²+½*2mr²/5*v²/r²
=½mv²+mv²/5
=7mv²/10
Equating the two we get,
7mv²/10 = mg(R-r)
→v² = 10g(R-r)/7
Now the radius of curvature for CoM of the ball at the bottom =R-r
Hence the centrifugal force on the ball P= mv²/(R-r)
=m*{10g(R-r)/7}/(R-r}
=10mg/7
Total force by the ball on the bottom of the cup = mg+P
=mg+10mg/7
=17mg/7
∴ Normal force by the cup on the ball when it reaches the bottom
=17mg/7
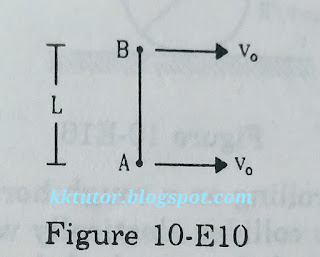
78. Figure (10-E14) shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.
ANSWER: For the ball to make a complete circle its weight must balance the centrifugal force at the top of the cylindrical part.
Let the set speed of the ball be v. The angular speed ⍵ = v/r.
The K. E. of the ball = ½mv²+½I⍵²
=½mv²+½*2mr²/5*v²/r²
=½mv²+mv²/5
=7mv²/10
Let the speed of the ball at the top position in the cylindrical part be v'.
Similarly, K.E. of the ball at this position = 7mv'²/10
The ball gains P.E. and loses K.E. to the same extent.
∴ 7mv²/10-7mv'²/10 = mg*2(R-r)
→v²-v'² = 20g(R-r)/7
→v'² = v²-20g(R-r)/7
For the required condition,
mv'²/(R-r) = mg
→v'² =g(R-r)
→v²-20g(R-r)/7 =g(R-r)
→v² =g(R-r)+20g(R-r)/7 =27g(R-r)/7
→v =√{27g(R-r)/7}
79. Figure (10-E15) shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and tangential accelerations of the center when the ball is at A.
(c) Find the normal force and the frictional force acting on the ball if H = 60 cm, R = 10 cm, θ = 0 and m = 70 g.
ANSWER: Since the ball is small it means r<<R {Where r is the radius of the ball}. And we shall assume that the ball moves in a circular path of radius R in the loop.
(a) We shall take the lowest point of the track as a reference level for the P.E. The P.E. of the ball at the release = mgH.
The P.E. of the ball at A = mg(R+R.sinθ)
The K.E. of the ball at A = The loss of the P.E.
= mgH-mg(R+R.sinθ)
=mg(H-R-R.sinθ)
(b) Suppose the center of the ball has a linear velocity v at point A, since the ball rolls its angular speed ⍵ =v/r. The K.E. of the ball in terms of v = ½mv²+ ½I⍵²
=½mv²+½*2mr²/5*v²/r² = ½mv²+mv²/5
=7mv²/10
Equating it with the K.E. expression in (a)
7mv²/10 = mg(H-R-R.sinθ)
v² = 10g(H-R-R.sinθ)/7 ................... (i)
Hence the radial acceleration = v²/R
= 10g(H-R-R.sinθ)/7R
=10g(H/R-1-Sinθ)/7
The tangential acceleration a = dv/dt
Differentiating (i) w.r.t. t
2v.dv/dt = (10g/7){0-0-Rcosθ.dθ/dt}
→2va = -10g⍵R.cosθ/7
→a = -5g⍵R.cosθ/7⍵R =-(5/7)g.cosθ
(c) With the given data,
v² = 10g(0.60-0.10-0.10.sin0°)/7
=5g/7
The normal force at A = mv²/R-mg.sinθ
= 0.070*5g/(7*0.10)-0.070g*sin0°
=g/2
=9.8/2
=4.9 N
At θ = 0° the ball is moving in upward direction and its tangential acceleration is a= -(5/7)g.cos0° = -5g/7 {from (b), the -ve sign is for downward direction i.e. retardation}
The direction of the frictional force F will be upwards as the ball moves in clockwise direction and the at the contact it will push the surface downward.
Hence, F-mg = ma =m(-5g/7)
→F = m(g-5g/7)
=2mg/7
=2*0.07*9.8/7
=0.02*9.8
=0.196 N Upwards
80. A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
ANSWER: Let the cue hit at a distance h above the center of the shell with a linear momentum MV.
When the shell sets in motion with a linear speed of the center v and angular speed ⍵, then for slip not to occur on the surface we have, v = r⍵
Since the linear momentum will be conserved MV = mv ......... (i)
[m = mass of the shell]
The angular momentum of the system before the strike about the center of the shell = MVh
The angular momentum of the shell about its center after the strike = I⍵
=(2mR²/3)*v/R
=2mvR/3
Since there is no external torque the angular momentum is conserved.
MVh = 2mvR/3
→mvh = 2mvR/3 {From (i)}
→h = 2R/3.
So the shell should be hit 2R/3 above the center.
81. A uniform wheel of radius R is set into rotation about its axis at an angular speed ⍵. This rotating wheel is now placed on a rough horizontal surface with its axis horizontal. Because of friction at the contact, the wheel accelerates forward and its rotation decelerates till the wheel starts pure rolling on the surface. Find the linear speed of the wheel after it starts pure rolling.
ANSWER: Let the mass of the wheel = m, the moment of inertia of the wheel about its rotational axis I = ½mR²
Hence its angular momentum P = I⍵ =½mR²⍵
When the wheel starts pure rolling, the point of contact remains stationary and the wheel rotates about an axis passing through the point of contact and parallel to the original axis (pure rotation). Hence the angular momentum of the wheel about this axis P' = I'⍵'
Let the linear speed of the wheel when it starts pure rolling = v, so its angular speed ⍵' = v/R. And I' = I + mR² =½mR²+mR² =3mR²/2
P' = 3mR²/2*v/R = 3mvR/2
Since in the absence of an external torque the angular momentum will be conserved, i.e. P' =P
→3mvR/2 = ½mR²⍵
→v = ⍵R/3
82. A thin spherical shell lying on a rough horizontal surface is hit by a cue in such a way that the line of action passes through the center of the shell. As a result, the shell starts moving with a linear speed v without any initial angular velocity. Find the linear speed of the shell after it starts pure rolling on the surface.
ANSWER: Let the linear speed be v' when it starts pure rolling, hence its angular speed about the point of contact, ⍵ = v'/r {r= radius and m = mass of the shell assumed}.
Initial angular momentum about the point of contact = mvr
Final angular momentum about the point of contact = I⍵
=(2mr²/3 + mr²)v'/r
=(5mr²/3)*v'/r
=5mrv'/3
Since the angular momentum will be conserved,
5mrv'/3 = mvr
→v' = 3v/5
83. A hollow sphere of radius R lies on a smooth horizontal surface. It is pulled by a horizontal force acting tangentially from the highest point. Find the distance traveled by the sphere during the time it makes one full rotation.
ANSWER: Let the tangential force be T. The acceleration of the sphere, a = T/m, where m = mass of the sphere.
The torque of the force about the center of the sphere = TR.
The angular acceleration α = TR/I =3TR/2mR² =3T/2mR
For a full rotation θ = 2π
Ifthe time taken in full rotation = t,
θ = 0*t + ½αt²
→½αt² = 2π
→½*3T/2mR*t² = 2π
→3Tt²/4mR = 2π
→t² = 8πmR/3T
The distance travelled = ut + ½at²
= 0 + ½*T/m*8πmR/3T
=4πR/3
84. A solid sphere of mass 0.50 kg is kept on a horizontal surface. The coefficient of static friction between the surface in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
ANSWER: µ = 2/7, m = 0.50 kg. Let the force applied at the top = F.
The torque of the force about the point of the contact = F*2R
=2FR
M.I. about the point of contact = 2mR²/5 + mR² = 7mR²/5
The angular acceleration α = 2FR/(7mR²/5)
=10F/7mR
For the sphere not to slip the linear acceleration of the CoM, a = αR = 10F/7m
The force of friction = P =µmg {in the forward direction, because the limiting force F produces a torque that pushes the surface at contact in backward direction}
∴F+P = ma
→F + µmg = m *10F/7m = 10F/7
→10F/7 - F = 2/7 * mg
→3F/7 = 2mg/7
→F = 2mg/3 = 2*0.50*9.8/3 ≈ 3.3 N
85. A solid sphere is set into motion on a rough horizontal surface with a linear speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown in the figure (10-E16). Find the linear speed of the sphere (a) when it stops rotating and (b) when slipping finally ceases and pure rolling starts.
ANSWER: (a) Let the mass of the sphere = m.
If the linear speed of the sphere when rotation stops is V,
Then, mvR-Iv/R = mVR
→mvR-2mR²/5 * v/R = mVR
→v - 2v/5 = V
→V = (5v-2v)/5
→V = 3v/5
(b) When the pure rolling starts, V' = ⍵'R
Now, mVR = I⍵'+mV'R = (2mR²/5)V'/R + mV'R
→mVR = 2mV'R/5 + mV'R
→V = 2V'/5 + V' = 7V'/5
→7V'/5 = V = 3v/5
→V' = (5/7)*(3v/5) = 3v/7
86. A solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
ANSWER: Since the collision is elastic, the rebound speed of the sphere = v. The vertical wall is smooth hence after rebound it will hold its angular momentum = I⍵ = Iv/ R. The angular momentum just after the strike about the contact point = mvR-Iv/R
(-ve because both have opposite direction)
=mvR-2mR²/5*v/R
=mvR-2mvR/5
=3mvR/5
If the speed of the sphere when pure rolling in backward direction starts = V, then the angular speed ⍵ = V/R.
Now the angular momentum = I⍵+mVR
= 2mR²/5*V/R +mVR
=2mVR/5 + mVR
=7mVR/5
Since the angular momentum will be conserved, hence
7mVR/5 = 3mvR/5
→7V = 3v
→V = 3v/7
ANSWER: Let the friction coefficient be µ. If the weight of the hollow sphere is m the normal force on it by the plane = mg.cosθ and hence the frictional force F = µmg.cosθ. The component of weight along the plane = mg.sinθ.
The torque on the ball due to frictional force about the point of contact = µmgr.cosθ {where r is the radius of the ball}
M.I. of the ball = 2mr²/3
(a) If the ball does not slide the angular acceleration of the ball,
α = µmgr.cosθ/2mr²/3
=3µg.cosθ/2r
With this angular acceleration the linear acceleration of the CoM (here the center of the sphere) a = αr = (3µg.cosθ/2r)*r =3µg.cosθ/2
If the sphere does not slide then the following condition should be satisfied
mg.sinθ-F =ma
mg.sinθ-µmg.cosθ =m3µg.cosθ/2
→sinθ = µ.cosθ+3µ.cosθ/2 =5µ.cosθ/2
→5µ.cosθ/2 = sinθ
→µ = 2.tanθ/5
(b) Now the frictional coefficient µ' =µ/2 = tanθ/5
Hence the frictional force F = µmg.cosθ
=mg.cosθ*tanθ/5
=mgsinθ/5
Torque on the ball = Fr=mgr.sinθ/5
α = Fr/I = (mgr.sinθ/5)/2mr²/3
=3g.sinθ/10r
Now mg.sinθ - F = ma
mg.sinθ - mg.sinθ/5 = ma
→a = 4g.sinθ/5
After moving distance l down the plane
v² = 0²+2al
→v = √(2al)
Also v = 0+at
→t = v/a =√(2al)/a =√(2l/a) =√(2l/4g.sinθ/5)
=√(5l/2g.sinθ)
And ⍵ = 0 +αt
=(3g.sinθ/10r)*√(5l/2g.sinθ)
=3{(5l)(g.sinθ)}1/2 /10r√2
The kinetic energy of the ball after it moves down a length l on the plane
=½mv²+½I⍵²
=
=ml*4g.sinθ/5+45mlg.sinθ/600
=4mlg.sinθ/5 +3mlg.sinθ/40
={(32+3)/40}mlg.sinθ
=(35/40)mlg.sinθ
=(7/8)mlg.sinθ
77. A Solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
ANSWER: Here our aim is to first find the velocity of the ball when it reaches the bottom of the cup. If the radius of the hemispherical cup is R, then K.E. of the ball at the bottom
= the loss in P.E. = mg(R-r) {Where m is the mass of the ball and the CoM of the ball will be r above the bottom}
But it is also = ½mv²+½I⍵²
=½mv²+½*2mr²/5*v²/r²
=½mv²+mv²/5
=7mv²/10
Equating the two we get,
7mv²/10 = mg(R-r)
→v² = 10g(R-r)/7
Now the radius of curvature for CoM of the ball at the bottom =R-r
Hence the centrifugal force on the ball P= mv²/(R-r)
=m*{10g(R-r)/7}/(R-r}
=10mg/7
Total force by the ball on the bottom of the cup = mg+P
=mg+10mg/7
=17mg/7
∴ Normal force by the cup on the ball when it reaches the bottom
=17mg/7
78. Figure (10-E14) shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.
 |
| Figure for Q-78 |
ANSWER: For the ball to make a complete circle its weight must balance the centrifugal force at the top of the cylindrical part.
Let the set speed of the ball be v. The angular speed ⍵ = v/r.
The K. E. of the ball = ½mv²+½I⍵²
=½mv²+½*2mr²/5*v²/r²
=½mv²+mv²/5
=7mv²/10
Let the speed of the ball at the top position in the cylindrical part be v'.
Similarly, K.E. of the ball at this position = 7mv'²/10
The ball gains P.E. and loses K.E. to the same extent.
∴ 7mv²/10-7mv'²/10 = mg*2(R-r)
→v²-v'² = 20g(R-r)/7
→v'² = v²-20g(R-r)/7
For the required condition,
mv'²/(R-r) = mg
→v'² =g(R-r)
→v²-20g(R-r)/7 =g(R-r)
→v² =g(R-r)+20g(R-r)/7 =27g(R-r)/7
→v =√{27g(R-r)/7}
79. Figure (10-E15) shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and tangential accelerations of the center when the ball is at A.
(c) Find the normal force and the frictional force acting on the ball if H = 60 cm, R = 10 cm, θ = 0 and m = 70 g.
 |
| Figure for Q-79 |
ANSWER: Since the ball is small it means r<<R {Where r is the radius of the ball}. And we shall assume that the ball moves in a circular path of radius R in the loop.
(a) We shall take the lowest point of the track as a reference level for the P.E. The P.E. of the ball at the release = mgH.
The P.E. of the ball at A = mg(R+R.sinθ)
The K.E. of the ball at A = The loss of the P.E.
= mgH-mg(R+R.sinθ)
=mg(H-R-R.sinθ)
(b) Suppose the center of the ball has a linear velocity v at point A, since the ball rolls its angular speed ⍵ =v/r. The K.E. of the ball in terms of v = ½mv²+ ½I⍵²
=½mv²+½*2mr²/5*v²/r² = ½mv²+mv²/5
=7mv²/10
Equating it with the K.E. expression in (a)
7mv²/10 = mg(H-R-R.sinθ)
v² = 10g(H-R-R.sinθ)/7 ................... (i)
Hence the radial acceleration = v²/R
= 10g(H-R-R.sinθ)/7R
=10g(H/R-1-Sinθ)/7
The tangential acceleration a = dv/dt
Differentiating (i) w.r.t. t
2v.dv/dt = (10g/7){0-0-Rcosθ.dθ/dt}
→2va = -10g⍵R.cosθ/7
→a = -5g⍵R.cosθ/7⍵R =-(5/7)g.cosθ
(c) With the given data,
v² = 10g(0.60-0.10-0.10.sin0°)/7
=5g/7
The normal force at A = mv²/R-mg.sinθ
= 0.070*5g/(7*0.10)-0.070g*sin0°
=g/2
=9.8/2
=4.9 N
At θ = 0° the ball is moving in upward direction and its tangential acceleration is a= -(5/7)g.cos0° = -5g/7 {from (b), the -ve sign is for downward direction i.e. retardation}
The direction of the frictional force F will be upwards as the ball moves in clockwise direction and the at the contact it will push the surface downward.
Hence, F-mg = ma =m(-5g/7)
→F = m(g-5g/7)
=2mg/7
=2*0.07*9.8/7
=0.02*9.8
=0.196 N Upwards
80. A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
ANSWER: Let the cue hit at a distance h above the center of the shell with a linear momentum MV.
When the shell sets in motion with a linear speed of the center v and angular speed ⍵, then for slip not to occur on the surface we have, v = r⍵
 |
| Figure for Q - 80 |
Since the linear momentum will be conserved MV = mv ......... (i)
[m = mass of the shell]
The angular momentum of the system before the strike about the center of the shell = MVh
The angular momentum of the shell about its center after the strike = I⍵
=(2mR²/3)*v/R
=2mvR/3
Since there is no external torque the angular momentum is conserved.
MVh = 2mvR/3
→mvh = 2mvR/3 {From (i)}
→h = 2R/3.
So the shell should be hit 2R/3 above the center.
81. A uniform wheel of radius R is set into rotation about its axis at an angular speed ⍵. This rotating wheel is now placed on a rough horizontal surface with its axis horizontal. Because of friction at the contact, the wheel accelerates forward and its rotation decelerates till the wheel starts pure rolling on the surface. Find the linear speed of the wheel after it starts pure rolling.
ANSWER: Let the mass of the wheel = m, the moment of inertia of the wheel about its rotational axis I = ½mR²
Hence its angular momentum P = I⍵ =½mR²⍵
When the wheel starts pure rolling, the point of contact remains stationary and the wheel rotates about an axis passing through the point of contact and parallel to the original axis (pure rotation). Hence the angular momentum of the wheel about this axis P' = I'⍵'
Let the linear speed of the wheel when it starts pure rolling = v, so its angular speed ⍵' = v/R. And I' = I + mR² =½mR²+mR² =3mR²/2
P' = 3mR²/2*v/R = 3mvR/2
Since in the absence of an external torque the angular momentum will be conserved, i.e. P' =P
→3mvR/2 = ½mR²⍵
→v = ⍵R/3
82. A thin spherical shell lying on a rough horizontal surface is hit by a cue in such a way that the line of action passes through the center of the shell. As a result, the shell starts moving with a linear speed v without any initial angular velocity. Find the linear speed of the shell after it starts pure rolling on the surface.
ANSWER: Let the linear speed be v' when it starts pure rolling, hence its angular speed about the point of contact, ⍵ = v'/r {r= radius and m = mass of the shell assumed}.
Initial angular momentum about the point of contact = mvr
Final angular momentum about the point of contact = I⍵
=(2mr²/3 + mr²)v'/r
=(5mr²/3)*v'/r
=5mrv'/3
Since the angular momentum will be conserved,
5mrv'/3 = mvr
→v' = 3v/5
83. A hollow sphere of radius R lies on a smooth horizontal surface. It is pulled by a horizontal force acting tangentially from the highest point. Find the distance traveled by the sphere during the time it makes one full rotation.
ANSWER: Let the tangential force be T. The acceleration of the sphere, a = T/m, where m = mass of the sphere.
The torque of the force about the center of the sphere = TR.
The angular acceleration α = TR/I =3TR/2mR² =3T/2mR
For a full rotation θ = 2π
Ifthe time taken in full rotation = t,
θ = 0*t + ½αt²
→½αt² = 2π
→½*3T/2mR*t² = 2π
→3Tt²/4mR = 2π
→t² = 8πmR/3T
The distance travelled = ut + ½at²
= 0 + ½*T/m*8πmR/3T
=4πR/3
84. A solid sphere of mass 0.50 kg is kept on a horizontal surface. The coefficient of static friction between the surface in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
ANSWER: µ = 2/7, m = 0.50 kg. Let the force applied at the top = F.
The torque of the force about the point of the contact = F*2R
=2FR
M.I. about the point of contact = 2mR²/5 + mR² = 7mR²/5
The angular acceleration α = 2FR/(7mR²/5)
=10F/7mR
For the sphere not to slip the linear acceleration of the CoM, a = αR = 10F/7m
The force of friction = P =µmg {in the forward direction, because the limiting force F produces a torque that pushes the surface at contact in backward direction}
∴F+P = ma
→F + µmg = m *10F/7m = 10F/7
→10F/7 - F = 2/7 * mg
→3F/7 = 2mg/7
→F = 2mg/3 = 2*0.50*9.8/3 ≈ 3.3 N
85. A solid sphere is set into motion on a rough horizontal surface with a linear speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown in the figure (10-E16). Find the linear speed of the sphere (a) when it stops rotating and (b) when slipping finally ceases and pure rolling starts.
 |
| Figure for Q-85 |
ANSWER: (a) Let the mass of the sphere = m.
If the linear speed of the sphere when rotation stops is V,
Then, mvR-Iv/R = mVR
→mvR-2mR²/5 * v/R = mVR
→v - 2v/5 = V
→V = (5v-2v)/5
→V = 3v/5
(b) When the pure rolling starts, V' = ⍵'R
Now, mVR = I⍵'+mV'R = (2mR²/5)V'/R + mV'R
→mVR = 2mV'R/5 + mV'R
→V = 2V'/5 + V' = 7V'/5
→7V'/5 = V = 3v/5
→V' = (5/7)*(3v/5) = 3v/7
86. A solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
ANSWER: Since the collision is elastic, the rebound speed of the sphere = v. The vertical wall is smooth hence after rebound it will hold its angular momentum = I⍵ = Iv/ R. The angular momentum just after the strike about the contact point = mvR-Iv/R
(-ve because both have opposite direction)
=mvR-2mR²/5*v/R
=mvR-2mvR/5
=3mvR/5
If the speed of the sphere when pure rolling in backward direction starts = V, then the angular speed ⍵ = V/R.
Now the angular momentum = I⍵+mVR
= 2mR²/5*V/R +mVR
=2mVR/5 + mVR
=7mVR/5
Since the angular momentum will be conserved, hence
7mVR/5 = 3mvR/5
→7V = 3v
→V = 3v/7
===<<<O>>>===
Links to the chapters -
ALL LINKS
CHAPTER- 10 - Rotational Mechanics
Questions for Short Answers
OBJECTIVE - I
OBJECTIVE - II
EXERCISES- Q-1 TO Q-15
EXERCISES- Q-16 TO Q-30
EXERCISES- Q-31 TO Q-45
EXERCISES- Q-46 TO Q-60
EXERCISES- Q-61 TO Q-75
CHAPTER- 10 - Rotational Mechanics
Questions for Short Answers
OBJECTIVE - I
OBJECTIVE - II
EXERCISES- Q-1 TO Q-15
EXERCISES- Q-16 TO Q-30
EXERCISES- Q-31 TO Q-45
EXERCISES- Q-46 TO Q-60
EXERCISES- Q-61 TO Q-75
CHAPTER- 9 - Center of Mass, Linear Momentum, Collision
HC Verma's Concepts of Physics, Chapter-8, WORK AND ENERGY
Click here for → Question for Short Answers
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → Exercises (1-10)
Click here for → Exercises (11-20)
Click here for → Exercises (21-30)
Click here for → Exercises (31-42)
Click here for → Exercise(43-54)
Click here for → Exercises (31-42)
Click here for → Exercise(43-54)
HC Verma's Concepts of Physics, Chapter-7, Circular Motion
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-30)
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-30)
HC Verma's Concepts of Physics, Chapter-6, Friction
Click here for → Friction OBJECTIVE-I
Click here for → Friction - OBJECTIVE-II
Click here for → Friction - OBJECTIVE-II
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
---------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-5, Newton's Law's of Motion
Click here for → QUESTIONS FOR SHORT ANSWER
Click here for→ Newton's laws of motion - Objective - I
Click here for → Newton's Laws of Motion - Objective -II
Click here for → Newton's Laws of Motion-Exercises(Q. No. 1 to 12)
Click here for→Newton's Laws of Motion,Exercises(Q.No. 13 to 27)
-------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-4, The Forces
"Questions for short Answers"
Click here for "The Forces" - OBJECTIVE-I
Click here for "The Forces" - OBJECTIVE-II
Click here for "The Forces" - Exercises
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------