My Channel on YouTube → SimplePhysics with KK
For links to
other chapters - See bottom of the page
Or click here → kktutor.blogspot.com
ROTATIONAL MECHANICS:--
OBJECTIVE - II
1. The axis of rotation of a purely rotating body
(a) must pass through the center of mass
(b) may pass through the center of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
ANSWER: (b), (d)
Explanation: It is not a necessary condition that the axis of rotation should pass through the center of mass or through a particle of the body. But it may pass through them.
2. Consider the following two equations
(A) L = I ⍵ (B) dL/dt = Γ
In noninertial frames
(a) both A and B are true
(b) A is true but B is false
(c) B is true but A is false
(d) both A and B are false
ANSWER: (b)
Explanation: dL/dt = total torque of external force, not equal to any torque. So dL/dt = Γ is not correct.
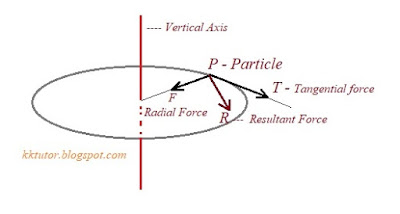
3. A particle moves on a straight line with a uniform velocity. Its angular momentum
(a) is always zero
(b) is zero about a point on the straight line
(c) is not zero about a point away from the straight line
(d) about any given point remains constant.
ANSWER: (b), (c), (d)
Explanation: The angular momentum of a particle about a point
=mvr {Where r is the perpendicular distance of the line of velocity from the point}
Since for a point on the line, r = 0, and for a point away from the line, r is not zero. Hence (b) and (c).
And for a given point r = constant, hence (d).
4. If there is no external force acting on a nonrigid body, which of the following quantities must remain constant
(a) angular momentum
(b) linear momentum
(c) kinetic energy
(d) moment of inertia.
ANSWER: (a), (b)
Explanation: If L be the angular momentum, then external torque = dL/dt
But given that it is zero, so dL/dt =0
→L = a constant.
Similarly, it can be shown that linear momentum = a constant.
(c) is not correct because in such situation total energy is constant.
(d) is not correct because the moment of Inertia does not depend upon the external force, it depends upon the shape and the axis of rotation. In a nonrigid body, these two may not remain constant.
5. Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the center of mass of the body but B does not.
(a) IA < IB
(b) If IA < IB, the axes are parallel
(c) If the axes are parallel, IA < IB
(d) If the axes are not parallel, IA ≥ IB.
ANSWER: (c)
Explanation: From the parallel axis theorem IB = IA + IA.r² where r is the distance between the parallel axes. Hence IA < IB.
Others are not necessary conditions.
6. A sphere is rotating about a diameter,
(a) The particles on the surface of the sphere do not have any linear acceleration.
(b) The particles on the diameter mentioned above do not have any linear acceleration.
(c) different particles on the surface have different angular speeds.
(d) All the particles on the surface have same linear speed.
ANSWER: (b)
Explanation: The particles on the surface of the sphere revolve in concentric circles. So, at least they have centripetal accelerations. (a) is not true.
Different particles on the surface take equal time to complete a revolution, hence they have equal angular speeds. So, (c) is not true.
The linear speed v = ɷr. That means the particles at different r will have different linear speed. So, (d) is not true.
Since for the particles on the diameter r = 0. So, v = 0. Since v is not changing so linear acceleration is zero. (b) is correct.
7. The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis through the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are
(a) angular acceleration
(b) angular velocity when the rod completes one rotation
(c) angular momentum when the rod completes one rotation
(d) torque of the applied force.
ANSWER: (d)
Explanation: The options (a), (b) and (c) involves the moment of Inertia which depends upon the pivoting end. Option (d) is unchanged because torque = F*l.
8. Consider a wheel of a bicycle rolling on a level road at a linear speed v₀ (Figure 10-Q4).
(a) The speed of the particle A is zero.
(b) The speed of B, C and D are all equal to v₀
(c) The speed of C is 2v₀.
(d) The speed of B is greater than the speed of O.
ANSWER: (a), (c), (d)
Explanation: The option (b) is not true because the wheel is not in pure rotation about O. It can be assumed that its diameter AC is instantaneously in pure rotation about A. So options (a) and (c) are correct. The point B has one more component of velocity downward, hence its total velocity > velocity of O. Hence option (d) also.
9. Two uniform solid spheres having unequal masses and unequal radii are released from the rest from the same height on a rough incline. If the spheres roll without slipping,
(a) the heavier sphere reaches the bottom first
(b) the bigger sphere reaches the bottom first
(c) the two spheres reach the bottom together
(d) the information given is not sufficient to tell which sphere will reach the bottom first.
ANSWER: (c)
Explanation: When the solid sphere rolls without slipping, its linear acceleration is given as, a =(5/7)g.sinΦ {where Φ is the angl of inclination with the horizontal plane.}
Clearly the linear acceleration is free of mass and the radius. So both the spheres will have equal accelerations and they will reach the bottom together.
10. A hollow sphere and a solid sphere having same mass and same radii are rolled down a rough inclined plane.
(a) the hollow sphere reaches the bottom first.
(b) the solid sphere reaches the bottom with greater speed.
(c) the solid sphere reaches the bottom with greater kinetic energy
(d) the two-sphere will reach the bottom with same linear momentum.
ANSWER: (b)
Explanation: For a hollow sphere, the linear acceleration
a = (3/5)g.sinΦ = 0.60g.sinΦ
For solid sphere
a = (5/7)g.sinΦ = 0.71g.sinΦ
Since 'a' for solid sphere is more so it will reach the bottom with a greater speed.
Since both the spheres are released from the same position, their initial potential energy mgh will be the same. So when they reach the bottom they lose same amount of P.E. and this loss of P.E. will be the gain in K.E. So both the spheres will have same K.E.at the bottom. Option (c) is not correct.
Since the solid sphere reaches the bottom with a greater speed and both have same mass, they can not have the same linear momentum. Thus option (d) is not correct.
11. A sphere can not roll on
(a) a smooth horizontal surface
(b) a smooth inclined surface
(c) a rough horizontal surface
(d) a rough inclined surface.
ANSWER: (b)
Explanation: On a smooth inclined surface there will be no friction to produce a torque, so no rolling.
12. In rear wheel drive cars, the engine rotates the rear wheels and the front wheels rotate only because the car moves. If such a car accelerates on a horizontal road, the friction
(a) on the rear wheels is in the forward direction.
(b) on the front wheels is in the backward direction.
(c) on the rear wheels has larger magnitude than the friction on the front wheels.
(d) on the car is in the backward direction.
ANSWER: (a), (b), (c)
Explanation: When accelerating the torque on the rear wheel tries the part in contact with the road to slide backward so the friction on it is forward. Option (a).
The body of the car tries to push the front wheel in the forward direction, hence the force of friction is in the backward direction. Option (b).
The driving rear wheel has to produce a force in the forward direction (through the torque) to push the whole mass of the car while the torque on the front wheel has just to overcome the inertia of the wheel. Hence the friction on the rear wheel is more than the front wheel. Option (c).
Net friction on the car is in forward direction because rear wheel friction is larger and in forward direction. Hence option (d) is not correct.
13. A sphere can roll on a surface inclined at an angle θ if the friction coefficient is more than (2/7)g.sinθ. Suppose the friction coefficient is (1/7)g.sinθ. If a sphere is released from rest on the incline,
(a) it will stay at rest
(b) it will make pure translation motion
(c) it will translate and rotate about the center
(d) the angular momentum of the sphere about its center will remain constant.
ANSWER: (c)
Explanation: Since there is some friction which will produce a torque on the sphere and there is no othe torque to balance it. Hnce the sphere will not stay at rest. Option (a) is not correct. Due to the torque produced by the friction it will have some rotational motion also. Hence option (b) is not correct.
From the question the friction coefficient is =(1/7)g.sinθ which is lessthan (2/7)g.sinθ {required for rolling only} so it will translate and rotate about the center. Option (c) is correct.
As the sphere go down the inclined plane its angular velocity will get increasing. So the angular momentum of the sphere about its center will continue increasing. Option (d) is not correct.
14. A sphere is rolled on a rough horizontal surface. It gradually slows down and stops. The force of friction tries to
(a) decrease the linear velocity
(b) increase the angular velocity
(c) increase the linear momentum
(d) decrease the angular velocity.
ANSWER: (a), (b)
Explanation: When a sphere is pushed on a rough horizontal surface to roll, it is given some linear speed and it ties to slip on the surface which is opposed by the force of friction so it tries to decrease yhe linear velocity and due to its direction it tries to increase the angular velocity. Hence option (a) and (b) and not the options (c) and (d).
15. Figure (10-Q5) shows a smooth inclined plane fixed in a car accelerating on a horizontal road. The angle of incline θ is related to the acceleration of the car as a = g.tanθ. If the sphere is set in pure rolling on the incline
(a) it will continue pure rolling
(b) it will slip down the plane
(c) its linear velocity will increase
(d) its linear velocity will decrease.
ANSWER: (a)
Explanation: To analize it we have to apply a pseudo force = ma in the opposite direction of a. Its component along the plane =ma.cosθ =mgtanθ.cosθ =mg.sinθ {towards up the incline}
Component of weight along the plane = mg.sinθ {towards down the plane}
So net force on the sphere along the plane = mg.sinθ - mg.sinθ = 0
The perpendicular component of the weight and pseudo force is balanced by the normal force.So it will continue pure rolling.
(a) must pass through the center of mass
(b) may pass through the center of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
ANSWER: (b), (d)
Explanation: It is not a necessary condition that the axis of rotation should pass through the center of mass or through a particle of the body. But it may pass through them.
2. Consider the following two equations
(A) L = I ⍵ (B) dL/dt = Γ
In noninertial frames
(a) both A and B are true
(b) A is true but B is false
(c) B is true but A is false
(d) both A and B are false
ANSWER: (b)
Explanation: dL/dt = total torque of external force, not equal to any torque. So dL/dt = Γ is not correct.
(a) is always zero
(b) is zero about a point on the straight line
(c) is not zero about a point away from the straight line
(d) about any given point remains constant.
ANSWER: (b), (c), (d)
Explanation: The angular momentum of a particle about a point
=mvr {Where r is the perpendicular distance of the line of velocity from the point}
Since for a point on the line, r = 0, and for a point away from the line, r is not zero. Hence (b) and (c).
And for a given point r = constant, hence (d).
4. If there is no external force acting on a nonrigid body, which of the following quantities must remain constant
(a) angular momentum
(b) linear momentum
(c) kinetic energy
(d) moment of inertia.
ANSWER: (a), (b)
Explanation: If L be the angular momentum, then external torque = dL/dt
But given that it is zero, so dL/dt =0
→L = a constant.
Similarly, it can be shown that linear momentum = a constant.
(c) is not correct because in such situation total energy is constant.
(d) is not correct because the moment of Inertia does not depend upon the external force, it depends upon the shape and the axis of rotation. In a nonrigid body, these two may not remain constant.
5. Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the center of mass of the body but B does not.
(a) IA < IB
(b) If IA < IB, the axes are parallel
(c) If the axes are parallel, IA < IB
(d) If the axes are not parallel, IA ≥ IB.
ANSWER: (c)
Explanation: From the parallel axis theorem IB = IA + IA.r² where r is the distance between the parallel axes. Hence IA < IB.
Others are not necessary conditions.
6. A sphere is rotating about a diameter,
(a) The particles on the surface of the sphere do not have any linear acceleration.
(b) The particles on the diameter mentioned above do not have any linear acceleration.
(c) different particles on the surface have different angular speeds.
(d) All the particles on the surface have same linear speed.
ANSWER: (b)
Explanation: The particles on the surface of the sphere revolve in concentric circles. So, at least they have centripetal accelerations. (a) is not true.
Different particles on the surface take equal time to complete a revolution, hence they have equal angular speeds. So, (c) is not true.
The linear speed v = ɷr. That means the particles at different r will have different linear speed. So, (d) is not true.
Since for the particles on the diameter r = 0. So, v = 0. Since v is not changing so linear acceleration is zero. (b) is correct.
7. The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis through the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are
(a) angular acceleration
(b) angular velocity when the rod completes one rotation
(c) angular momentum when the rod completes one rotation
(d) torque of the applied force.
ANSWER: (d)
Explanation: The options (a), (b) and (c) involves the moment of Inertia which depends upon the pivoting end. Option (d) is unchanged because torque = F*l.
8. Consider a wheel of a bicycle rolling on a level road at a linear speed v₀ (Figure 10-Q4).
(a) The speed of the particle A is zero.
(b) The speed of B, C and D are all equal to v₀
(c) The speed of C is 2v₀.
(d) The speed of B is greater than the speed of O.
 |
| Figure for Q-8 |
ANSWER: (a), (c), (d)
Explanation: The option (b) is not true because the wheel is not in pure rotation about O. It can be assumed that its diameter AC is instantaneously in pure rotation about A. So options (a) and (c) are correct. The point B has one more component of velocity downward, hence its total velocity > velocity of O. Hence option (d) also.
9. Two uniform solid spheres having unequal masses and unequal radii are released from the rest from the same height on a rough incline. If the spheres roll without slipping,
(a) the heavier sphere reaches the bottom first
(b) the bigger sphere reaches the bottom first
(c) the two spheres reach the bottom together
(d) the information given is not sufficient to tell which sphere will reach the bottom first.
ANSWER: (c)
Explanation: When the solid sphere rolls without slipping, its linear acceleration is given as, a =(5/7)g.sinΦ {where Φ is the angl of inclination with the horizontal plane.}
Clearly the linear acceleration is free of mass and the radius. So both the spheres will have equal accelerations and they will reach the bottom together.
(a) the hollow sphere reaches the bottom first.
(b) the solid sphere reaches the bottom with greater speed.
(c) the solid sphere reaches the bottom with greater kinetic energy
(d) the two-sphere will reach the bottom with same linear momentum.
ANSWER: (b)
Explanation: For a hollow sphere, the linear acceleration
a = (3/5)g.sinΦ = 0.60g.sinΦ
For solid sphere
a = (5/7)g.sinΦ = 0.71g.sinΦ
Since 'a' for solid sphere is more so it will reach the bottom with a greater speed.
Since both the spheres are released from the same position, their initial potential energy mgh will be the same. So when they reach the bottom they lose same amount of P.E. and this loss of P.E. will be the gain in K.E. So both the spheres will have same K.E.at the bottom. Option (c) is not correct.
Since the solid sphere reaches the bottom with a greater speed and both have same mass, they can not have the same linear momentum. Thus option (d) is not correct.
11. A sphere can not roll on
(a) a smooth horizontal surface
(b) a smooth inclined surface
(c) a rough horizontal surface
(d) a rough inclined surface.
ANSWER: (b)
Explanation: On a smooth inclined surface there will be no friction to produce a torque, so no rolling.
12. In rear wheel drive cars, the engine rotates the rear wheels and the front wheels rotate only because the car moves. If such a car accelerates on a horizontal road, the friction
(a) on the rear wheels is in the forward direction.
(b) on the front wheels is in the backward direction.
(c) on the rear wheels has larger magnitude than the friction on the front wheels.
(d) on the car is in the backward direction.
ANSWER: (a), (b), (c)
Explanation: When accelerating the torque on the rear wheel tries the part in contact with the road to slide backward so the friction on it is forward. Option (a).
The body of the car tries to push the front wheel in the forward direction, hence the force of friction is in the backward direction. Option (b).
The driving rear wheel has to produce a force in the forward direction (through the torque) to push the whole mass of the car while the torque on the front wheel has just to overcome the inertia of the wheel. Hence the friction on the rear wheel is more than the front wheel. Option (c).
Net friction on the car is in forward direction because rear wheel friction is larger and in forward direction. Hence option (d) is not correct.
13. A sphere can roll on a surface inclined at an angle θ if the friction coefficient is more than (2/7)g.sinθ. Suppose the friction coefficient is (1/7)g.sinθ. If a sphere is released from rest on the incline,
(a) it will stay at rest
(b) it will make pure translation motion
(c) it will translate and rotate about the center
(d) the angular momentum of the sphere about its center will remain constant.
ANSWER: (c)
Explanation: Since there is some friction which will produce a torque on the sphere and there is no othe torque to balance it. Hnce the sphere will not stay at rest. Option (a) is not correct. Due to the torque produced by the friction it will have some rotational motion also. Hence option (b) is not correct.
From the question the friction coefficient is =(1/7)g.sinθ which is lessthan (2/7)g.sinθ {required for rolling only} so it will translate and rotate about the center. Option (c) is correct.
As the sphere go down the inclined plane its angular velocity will get increasing. So the angular momentum of the sphere about its center will continue increasing. Option (d) is not correct.
(a) decrease the linear velocity
(b) increase the angular velocity
(c) increase the linear momentum
(d) decrease the angular velocity.
ANSWER: (a), (b)
Explanation: When a sphere is pushed on a rough horizontal surface to roll, it is given some linear speed and it ties to slip on the surface which is opposed by the force of friction so it tries to decrease yhe linear velocity and due to its direction it tries to increase the angular velocity. Hence option (a) and (b) and not the options (c) and (d).
(a) it will continue pure rolling
(b) it will slip down the plane
(c) its linear velocity will increase
(d) its linear velocity will decrease.
 |
| Figure for Q-15 |
ANSWER: (a)
Explanation: To analize it we have to apply a pseudo force = ma in the opposite direction of a. Its component along the plane =ma.cosθ =mgtanθ.cosθ =mg.sinθ {towards up the incline}
 |
| Figure for Q-15 |
So net force on the sphere along the plane = mg.sinθ - mg.sinθ = 0
The perpendicular component of the weight and pseudo force is balanced by the normal force.So it will continue pure rolling.
===<<<O>>>===
Links to the chapters -
ALL LINKS
CHAPTER- 10 - Rotational Mechanics
Questions for Short Answers
OBJECTIVE - I
OBJECTIVE - II
EXERCISES - Q-1 TO Q-15
EXERCISES - Q-16 TO Q-30
CHAPTER- 10 - Rotational Mechanics
Questions for Short Answers
OBJECTIVE - I
OBJECTIVE - II
EXERCISES - Q-1 TO Q-15
EXERCISES - Q-16 TO Q-30
CHAPTER- 9 - Center of Mass, Linear Momentum, Collision
HC Verma's Concepts of Physics, Chapter-8, WORK AND ENERGY
Click here for → Question for Short Answers
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → Exercises (1-10)
Click here for → Exercises (11-20)
Click here for → Exercises (21-30)
Click here for → Exercises (31-42)
Click here for → Exercise(43-54)
Click here for → Exercises (31-42)
Click here for → Exercise(43-54)
HC Verma's Concepts of Physics, Chapter-7, Circular Motion
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-30)
Click here for → OBJECTIVE-I
Click here for → OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-30)
HC Verma's Concepts of Physics, Chapter-6, Friction
Click here for → Friction OBJECTIVE-I
Click here for → Friction - OBJECTIVE-II
Click here for → Friction - OBJECTIVE-II
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (1-10)
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
---------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-5, Newton's Law's of Motion
Click here for → QUESTIONS FOR SHORT ANSWER
Click here for→ Newton's laws of motion - Objective - I
Click here for → Newton's Laws of Motion - Objective -II
Click here for → Newton's Laws of Motion-Exercises(Q. No. 1 to 12)
Click here for→Newton's Laws of Motion,Exercises(Q.No. 13 to 27)
-------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-4, The Forces
"Questions for short Answers"
Click here for "The Forces" - OBJECTIVE-I
Click here for "The Forces" - OBJECTIVE-II
Click here for "The Forces" - Exercises
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------