My Channel on You Tube ---> SimplePhysics with KK
For links to other chapters - See bottom of the page
EXERCISES (1-10)
1. A body slipping on a rough horizontal plane moves with a deceleration of 4.0 m/s². What is the coefficient of kinetic friction between the block and the plane ?
Answer: The friction force causing the deceleration = f = m.a
Where m = mass of the body,
and a = deceleration of the body = 4.0 m/s²
So f = 4m N
Normal force on the body = weight of the body = mg N
So coefficient of kinetic friction = 4m/mg =4/g = 4/9.8 = 0.4
2. A block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest ?
Answer: Let mass of the block be m . Weight of block =mg
So, Normal force on the block N =mg, Given µ=0.10
→Force of friction f =µ.N =0.10*mg
This force of friction will try to stop the block with retardation a=Force/mass =0.10*mg/m =0.10*g =0.10*9.8 =0.98 m/s²
Now initial velocity of the block = u =10 m/s
Final velocity = 0, a=-0.98 m/s², s= distance traveled =?
Using the relation v²=u²+2as
we get, 0²=10²-2*0.98*s →2*0.98s= 100 →s=100/1.96 m =51 m
3. A block of mass m is kept on a horizontal table. If the static friction coefficient is µ , find the frictional force acting on the block ?
So, Normal force on the block N =mg, Given µ=0.10
→Force of friction f =µ.N =0.10*mg
This force of friction will try to stop the block with retardation a=Force/mass =0.10*mg/m =0.10*g =0.10*9.8 =0.98 m/s²
Now initial velocity of the block = u =10 m/s
Final velocity = 0, a=-0.98 m/s², s= distance traveled =?
Using the relation v²=u²+2as
we get, 0²=10²-2*0.98*s →2*0.98s= 100 →s=100/1.96 m =51 m
3. A block of mass m is kept on a horizontal table. If the static friction coefficient is µ , find the frictional force acting on the block ?
Answer: Since the block is only kept on the horizontal surface and no force is applied on it trying to move, so force of friction is zero because frictional force comes in to action only when the surfaces in contact are in relative motion or trying to slip over each other.
4. A block slides down an inclined surface of inclination 30° with the horizontal. Starting from rest it covers 8 m in first two seconds. Find the coefficient of kinetic friction between the two.
Answer: Let us first find the acceleration of the block = a
We have, initial velocity = u = 0, Distance traveled = s = 8 m
time = t = 2 s, From the relation s=ut+½at²,
we get 8=0+½a*2² =2a →a = 4 m/s²
So the net force on the block along the incline = m.a =m.4 =4.m
But this net force from the diagram below = mg.sin30°-f
=½mg-f
Equating these two, ½mg-f = 4.m
→f=½*9.8m-4m
=4.9m-4m=0.9m
Normal force on the block = mg.cos30° =√3/2*9.8m =8.48m
So coefficient of kinetic friction =0.9m/8.48m =0.11
5. Suppose the block of the previous problem is pushed down the incline with a force of 4 N. How far will the block move in the first two seconds after starting from rest? The mass of block is 4 kg.
Answer: In the previous problem when there is no external force, net force along the incline is =mg.sin30°-f N where m = mass of the block. In this problem when m = 4 kg and and external force along the incline = 4 N, f=0.9m,
Net force along the incline = mg.sin30°-f+4 N
=4*9.8*½-0.9*4+4 N
=19.6-3.6+4 N
=20 N
So acceleration along the incline, a = Force/mass = 20/4 =5 m/s²
Given t=2 s, using the relation, distance traveled s=ut+½at²
=0+½*5*2² = 10 m
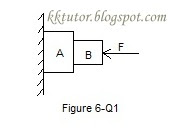
6. A body of mass 2 kg is lying on a rough inclined plane of inclination 30°. Find the magnitude of the force parallel to the incline needed to make the block move (a) up the incline (b) down the incline. Coefficient of static friction=0.2.
Answer: The only force acting on the block trying to move it down the plane is the component of its weight = mg.sinΦ
{where Φ=30° (angle of inclination) and m= 2 kg (mass of the block)}
=2*9.8*sin30° =19.6*½ =9.8 N
To move the block in either direction the net force along the plane in that direction must be just more than the limiting force of friction So let us first find this Limiting frictional force f which is equal to µR where R = Normal force on the block.
Normal force on the block is equal to component of the weight perpendicular to the plane = mg.cosΦ = 2*9.8*cos30° =2*9.8*√3/2 =9.8√3
Limiting frictional force f = µR = 0.2*9.8√3 =3.394 N
(Given µ=0.2)
(a) To move the block up the incline
Net force opposing the movement = Limiting frictional force+Component of weight along the incline
=3.394+9.8 N
=13.194 N
So to move the block up the incline should be just more than this force =13.194 N ≈13.2 N
(b) To move the block down the incline
Since the component of weight which tries to move the block down the plane is more than the limiting frictional force (9.8>3.394), so no external force is needed to move the block down the incline. It will move itself.
i.e. external force needed to move the block down the incline =zero.
7. Repeat part (a) of problem 6 if the push is applied horizontally and not parallel to the incline.
Answer: Let a push of F Newton is applied horizontally to move the block up the incline. Now a component of F = Fsin30° will also be added to the weight component mgcos30° pushing the block perpendicular to the plane, See the diagram below:--
so now the Normal force R= mgcos30°+Fsin30° and the Limiting frictional force f =µR =µ(mgcos30°+Fsin30°)
Total force acting down the incline on the block
=Limiting Frictional force+weight component down the incline
= µ(mgcos30°+Fsin30°)+mg.sin30° .......(i)
To move the block up the incline the component of push along the incline (Fcos30°) should be equal to this force ..(i)
Equating the two we get
Fcos30°= µ(mgcos30°+Fsin30°)+mg.sin30°
Solve this equation for F, which only is unknown in it,
→Fcos30°=µmg.cos30°+µFsin30°+mg.sin30°
→F(cos30°-µsin30°)= µmg.cos30°+mg.sin30°
→F(√3/2-0.20*½)=0.20*2*9.8*√3/2+ 2*9.8*1/2
→F(1.732-0.20)/2=0.20*9.8*1.732+9.8
→0.766F=13.195
→F=13.195/0.766 =17.23 N
8. In a children park an inclined plane is constructed with an angle of incline 45° in the middle part (figure 6-E1). Find the acceleration of a boy sliding on it if the friction coefficient between the cloth of the boy and the incline is 0.6 and g=10 m/s².
Answer: Let mass of boy be M.
Normal force on the boy =Component of weight perpendicular to the plane = Mg.cos45°
Frictional force on the boy =µMg.cos45°
Component of weight along the plane = Mg.sin45°
Net force on the boy down the incline = Mg.sin45°-µMg.cos45°
=Mg(1/√2-0.6/√2) =(0.4/√2)*Mg
Acceleration of the boy =Force/mass = (0.4/√2)*g =0.4*10/√2
=4/√2 =4√2/2 =2√2 m/s²
=2*1.41 =2.82 m/s²
9. A body starts slipping down an incline and moves half meter in half second. How long will it take it to move the next half meter?
Answer: This problem has nothing to do with friction. From the given data we need to calculate the acceleration of the body and then calculate the unknown. Here we have,
Initial velocity u= 0 , Time taken =0.5 s, Distance traveled s=0.5 m,
To find acceleration 'a' we use the relation s=ut+½at²
→ 0.5=0+½.a*(0.5)²
→ 0.5=0.5*a*(0.5)²
→ a=1/(0.5)² =4 m/s²
Let us calculate the time taken by the body to travel 1 m from the beginning, Now s=1 m, u=0, a=4 m/s², t=?
1=0+½*4*t² = 2t²
→t²=1/2
→t=√(0.5)= 0.71 s
So to travel 1 m distance time taken is 0.71 s while given that time taken to travel first half meter =0.5 s; Hence time taken to travel next half meter =0.71-0.5 s = 0.21 s
10. The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that if λ be the angle of friction and µ the coefficient of static friction, λ≤ tan-1µ .
4. A block slides down an inclined surface of inclination 30° with the horizontal. Starting from rest it covers 8 m in first two seconds. Find the coefficient of kinetic friction between the two.
Answer: Let us first find the acceleration of the block = a
We have, initial velocity = u = 0, Distance traveled = s = 8 m
time = t = 2 s, From the relation s=ut+½at²,
we get 8=0+½a*2² =2a →a = 4 m/s²
So the net force on the block along the incline = m.a =m.4 =4.m
But this net force from the diagram below = mg.sin30°-f
=½mg-f
 |
| Diagram for Problem-4 |
Equating these two, ½mg-f = 4.m
→f=½*9.8m-4m
=4.9m-4m=0.9m
Normal force on the block = mg.cos30° =√3/2*9.8m =8.48m
So coefficient of kinetic friction =0.9m/8.48m =0.11
5. Suppose the block of the previous problem is pushed down the incline with a force of 4 N. How far will the block move in the first two seconds after starting from rest? The mass of block is 4 kg.
Answer: In the previous problem when there is no external force, net force along the incline is =mg.sin30°-f N where m = mass of the block. In this problem when m = 4 kg and and external force along the incline = 4 N, f=0.9m,
Net force along the incline = mg.sin30°-f+4 N
=4*9.8*½-0.9*4+4 N
=19.6-3.6+4 N
=20 N
So acceleration along the incline, a = Force/mass = 20/4 =5 m/s²
Given t=2 s, using the relation, distance traveled s=ut+½at²
=0+½*5*2² = 10 m
6. A body of mass 2 kg is lying on a rough inclined plane of inclination 30°. Find the magnitude of the force parallel to the incline needed to make the block move (a) up the incline (b) down the incline. Coefficient of static friction=0.2.
Answer: The only force acting on the block trying to move it down the plane is the component of its weight = mg.sinΦ
{where Φ=30° (angle of inclination) and m= 2 kg (mass of the block)}
=2*9.8*sin30° =19.6*½ =9.8 N
To move the block in either direction the net force along the plane in that direction must be just more than the limiting force of friction So let us first find this Limiting frictional force f which is equal to µR where R = Normal force on the block.
Normal force on the block is equal to component of the weight perpendicular to the plane = mg.cosΦ = 2*9.8*cos30° =2*9.8*√3/2 =9.8√3
Limiting frictional force f = µR = 0.2*9.8√3 =3.394 N
(Given µ=0.2)
(a) To move the block up the incline
Net force opposing the movement = Limiting frictional force+Component of weight along the incline
=3.394+9.8 N
=13.194 N
So to move the block up the incline should be just more than this force =13.194 N ≈13.2 N
(b) To move the block down the incline
Since the component of weight which tries to move the block down the plane is more than the limiting frictional force (9.8>3.394), so no external force is needed to move the block down the incline. It will move itself.
i.e. external force needed to move the block down the incline =zero.
7. Repeat part (a) of problem 6 if the push is applied horizontally and not parallel to the incline.
Answer: Let a push of F Newton is applied horizontally to move the block up the incline. Now a component of F = Fsin30° will also be added to the weight component mgcos30° pushing the block perpendicular to the plane, See the diagram below:--
 |
| Diagram for Answer - 7 |
so now the Normal force R= mgcos30°+Fsin30° and the Limiting frictional force f =µR =µ(mgcos30°+Fsin30°)
Total force acting down the incline on the block
=Limiting Frictional force+weight component down the incline
= µ(mgcos30°+Fsin30°)+mg.sin30° .......(i)
To move the block up the incline the component of push along the incline (Fcos30°) should be equal to this force ..(i)
Equating the two we get
Fcos30°= µ(mgcos30°+Fsin30°)+mg.sin30°
Solve this equation for F, which only is unknown in it,
→Fcos30°=µmg.cos30°+µFsin30°+mg.sin30°
→F(cos30°-µsin30°)= µmg.cos30°+mg.sin30°
→F(√3/2-0.20*½)=0.20*2*9.8*√3/2+ 2*9.8*1/2
→F(1.732-0.20)/2=0.20*9.8*1.732+9.8
→0.766F=13.195
→F=13.195/0.766 =17.23 N
8. In a children park an inclined plane is constructed with an angle of incline 45° in the middle part (figure 6-E1). Find the acceleration of a boy sliding on it if the friction coefficient between the cloth of the boy and the incline is 0.6 and g=10 m/s².
 |
| Figure for Problem-8 |
Answer: Let mass of boy be M.
Normal force on the boy =Component of weight perpendicular to the plane = Mg.cos45°
Frictional force on the boy =µMg.cos45°
Component of weight along the plane = Mg.sin45°
Net force on the boy down the incline = Mg.sin45°-µMg.cos45°
=Mg(1/√2-0.6/√2) =(0.4/√2)*Mg
Acceleration of the boy =Force/mass = (0.4/√2)*g =0.4*10/√2
=4/√2 =4√2/2 =2√2 m/s²
=2*1.41 =2.82 m/s²
9. A body starts slipping down an incline and moves half meter in half second. How long will it take it to move the next half meter?
Answer: This problem has nothing to do with friction. From the given data we need to calculate the acceleration of the body and then calculate the unknown. Here we have,
Initial velocity u= 0 , Time taken =0.5 s, Distance traveled s=0.5 m,
To find acceleration 'a' we use the relation s=ut+½at²
→ 0.5=0+½.a*(0.5)²
→ 0.5=0.5*a*(0.5)²
→ a=1/(0.5)² =4 m/s²
Let us calculate the time taken by the body to travel 1 m from the beginning, Now s=1 m, u=0, a=4 m/s², t=?
1=0+½*4*t² = 2t²
→t²=1/2
→t=√(0.5)= 0.71 s
So to travel 1 m distance time taken is 0.71 s while given that time taken to travel first half meter =0.5 s; Hence time taken to travel next half meter =0.71-0.5 s = 0.21 s
10. The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that if λ be the angle of friction and µ the coefficient of static friction, λ≤ tan-1µ .
Answer: See the diagram below:-

Diagram for Answer - 10

F=Resultant contact force and λ=angle of friction,
Normal force R = F.cosλ and frictional force f=F.sinλ
But the limiting frictional force =µR =µF.cosλ , which will be always greater than or equal to frictional force f= F.sinλ,
i.e. f≤ µR
→F.sinλ ≤ µF.cosλ
→tanλ≤µ
→ λ ≤ tan-1µ
===<<O>>===
HC Verma's Concepts of Physics, Chapter-7, Circular Motion,
Click here for → Questions for short Answer
Click here for → Objective I
Click here for → Objective II
Click here for → Exercises (1-10)
Click here for → Exercises (11-20)
Click here for → Exercises (21-30)
HC Verma's Concepts of Physics, Chapter-6, Friction,
Click here for → Questions for Short Answer
Click here for → OBJECTIVE-I
Click here for → Friction OBJECTIVE-II
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
------------------------------------------------------------------------------ Click here for → Friction OBJECTIVE-II
Click here for → Exercises (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
HC Verma's Concepts of Physics, Chapter-5, Newton's Law's of Motion
Click here for → QUESTIONS FOR SHORT ANSWER
Click here for→ Newton's laws of motion - Objective - I
Click here for → Newton's Laws of Motion - Objective -II
Click here for → Newton's Laws of Motion-Exercises(Q. No. 1 to 12)
Click here for→Newton's Laws of Motion,Exercises(Q.No. 13 to 27)
-------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-4, The Forces
"Questions for short Answers"
Click here for "The Forces" - OBJECTIVE-I
Click here for "The Forces" - OBJECTIVE-II
Click here for "The Forces" - Exercises
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------