My Channel on You Tube ---> SimplePhysics with KK
For links to
other chapters - See bottom of the page
OBJECTIVE-I
1. In a situation the contact force by a rough horizontal surface on a body placed on it has constant magnitude. If the angle between this force and the vertical is decreased, the frictional force between the surface and the body will
(i) increase (ii) decrease
(iii) remain the same (iv) may increase or decrease
Answer: (ii) decrease
Explanation: Let the magnitude of contact force be F and angle between F and vertical be Θ. The vertical and horizontal components of this contact force F are Normal force and Friction force respectively. See the figure below:-
 |
| Figure for Answer no-1 |
Friction force= F.sinΘ
As Θ decreases the value of sinΘ also decreases. Since given that F is constant, so F.sinΘ i.e. Friction force also decreases.
2. While walking on ice, one should take small steps to avoid slipping. This is because small steps ensure
(a) larger friction (b) smaller friction
(c) larger normal force (c) smaller normal force
Answer: (b) smaller friction
Explanation: Small steps keep the angle between the leg and the vertical small i.e. angle between the contact force and vertical is small so the horizontal component of the contact force (Friction force) is small. The reason being the same as in question 1.
3. A body of mass M is kept on a rough horizontal surface (friction coefficient = µ). A person is trying to pull the body by applying a horizontal force but the body is not moving. The force by the surface on A is F where
(a) F=Mg (b) F = µ Mg
(c) Mg ≤ F ≤ Mg√(1+µ2) (d) Mg ≥ F ≥ Mg√(1-µ2)
Answer: (c) Mg ≤ F ≤ Mg√(1+µ2)
Explanation:
Weight of the body Mg = Normal force on the body by the surface
Let pull by the person be P. Then the value of P ≤ µMg.
Force by the surface on A = F = √{(P)²+(Mg)²}
For Maximum F, P = µMg
So, Fmax = √{(µMg)²+(Mg)²} = Mg√(1+µ²)i.e. F≤ Fmax
→ F≤ Mg√(1+µ²) ..................... (i)
Now F = Mg.secΘ [Where Θ is the angle between F and vertical, See figure below]
 |
| Figure for Answer no-3 |
Since secΘ≥1
→Mg.secΘ≥Mg
→F≥Mg
→Mg≤F ..........................................(ii)
Combine (i) and (ii) and we get,
Mg≤F≤ Mg√(1+µ²)
4. A scooter starting from rest moves with a constant acceleration for a time Δt1, then with a constant velocity for the next Δt2, and finally with a constant deceleration for the next Δt3, to come to rest. A 500 N man sitting on the scooter behind the driver manages to stay at rest with respect to the scooter without touching any other part. The force exerted by the seat on the man is
(a) 500 N throughout the journey
(b) less than 500 N throughout the journey
(c) more than 500 N throughout the journey
(d) > 500 N for the time Δt1, and Δt3 and 500N for Δt2.
Answer: (d) > 500 N for the time Δt1, and Δt3 and 500N for Δt2. Explanation: During the constant velocity for time Δt2 there is no relative movement between the man and the seat and only force applied by the seat on the man is Normal Force which is equal to weight of the man =500 N.
But during the acceleration (Δt1) and deceleration (Δt3) the seat exerts an addition force of friction on man in horizontal direction. Let this be F. Now the force by seat on man is resultant of 500 N and F,
=√{(500)²+F²} N, which is >500 N.
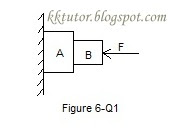
5. Consider the situation shown in figure (6-Q1). The wall is smooth but the surface of A and B in contact are rough. The friction on B due to A in equilibrium
(c) is zero (d) the system cannot remain in equilibrium.
Answer: (d) the system cannot remain in equilibrium.
Explanation: Since the wall is smooth, there is no force to counter the weight of the blocks i.e. sum of forces in vertical direction is not zero, Hence the system cannot remain in equilibrium.
6. Suppose all the surfaces in the previous problem are rough. The direction of friction on B due to A
(a) is upward (b) is downward
(c) is zero (d) depends on the masses of A and B
Answer: (a) is upward
Explanation: At equilibrium the weight of block B (Downward force) has to be balanced by an upward force which is the force of friction applied by block A on B.
7. Two cars of unequal masses use similar tyres. If they are moving with the same initial speed the minimum slipping distance
(a) is smaller for heavier car
(b) is smaller for lighter car
(c) is same for both cars
(d) depends on the volume of the car
Answer: (c) is same for both cars
Explanation: During slipping, the force of friction on a car
= µMg
(where M is the mass of the car and µ is the coefficient of kinetic friction.)
The deceleration = Force/mass = µMg/M =µg
This expression for deceleration is independent of M (Mass of the car), so the minimum slipping distance is same for both cars.
8. In order to stop a car in shortest distance on a horizontal road, one should
(a) apply the brakes very hard so that the wheels stop rotating
(b) Apply the brakes hard enough to just prevent slipping
(c) pump the brakes (press and release)
(d) shut the engines off and not apply brakes
Answer: (b) Apply the brakes hard enough to just prevent slipping
Explanation: In order to stop a car in shortest distance on a horizontal road, Maximum possible force of friction by applying brakes is needed. Maximum force of friction can only be achieved when the surfaces in contact are just on the verge of slipping but do not slip. In this situation the limiting/maximum static force of friction come into action. So apply the brakes hard enough to just prevent slipping.
9. A block A kept on an inclined surface just begins to slide if the inclination is 30°. The block is replaced by another block B and it is found that it just begins to slide if the inclination is 40°.
(a) mass of A > mass of B
(b) mass of A < mass of B
(c) mass of A = mass of B
(d) all the three are possible
Answer: (d) all the three are possible
Explanation: It is the case of maximum static friction. The blocks begin to slide if the coefficient of static friction µ = tanΘ, irrespective of their masses. So, all the three situations are possible.
10. A boy of mass M is applying a horizontal force to slide a box of mass M' on a rough horizontal surface. the coefficient of friction between shoes of the boy and the floor is µ and that between the box and the floor is µ'. In which of the following cases it is certainly not possible to slide the box?
(a) µ<µ', M<M' (b) µ>µ', M<M'
(b) µ<µ', M>M' (d) µ>µ', M>M'
Answer: (a) µ<µ', M<M'
Explanation: The force applied by the boy on the box is equal to the force of friction between the shoes of the boy and the floor which is equal to µMg.
Force of friction between the box and the floor = µ'M'g.
To slide the box µMg>µ'M'g
→ µM>µ'M'
This is not possible only if µ<µ', M<M'
Force of friction between the box and the floor = µ'M'g.
To slide the box µMg>µ'M'g
→ µM>µ'M'
This is not possible only if µ<µ', M<M'
===<<<O>>>===
Links for the chapters -
HC Verma's Concepts of Physics, Chapter-7, Circular Motion,
Click here for → Questions for short Answer
Click here for → Objective I
Click here for → Objective II
Click here for → Exercises (1-10)
Click here for → Exercises (11-20)
Click here for → Exercises (21-30)
HC Verma's Concepts of Physics, Chapter-6, Friction,
Click here for → Questions for Short Answer
Click here for → Friction - OBJECTIVE-II
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
Click here for → EXERCISES (11-20)
Click here for → EXERCISES (21-31)
For more practice on problems on friction solve these "New Questions on Friction" .
--------------------------------------------------
HC Verma's Concepts of Physics, Chapter-5, Newton's Law's of Motion
Click here for → QUESTIONS FOR SHORT ANSWER
Click here for→ Newton's laws of motion - Objective - I
Click here for → Newton's Laws of Motion - Objective -II
Click here for → Newton's Laws of Motion-Exercises(Q. No. 1 to 12)
Click here for→Newton's Laws of Motion,Exercises(Q.No. 13 to 27)
-------------------------------------------------------------------------------
HC Verma's Concepts of Physics, Chapter-4, The Forces
"Questions for short Answers"
Click here for "The Forces" - OBJECTIVE-I
Click here for "The Forces" - OBJECTIVE-II
Click here for "The Forces" - Exercises
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------
Sir, in first question
ReplyDeletefriction force =uN=u(mg+ f cos(x)) where x is the angle made b'twn vertical and force, so as x decreases cosx increase so friction also..
is it like this?
sir, thank you for uploading the answers for all the questions in your blog. it is really helpful and saves my time...
ReplyDeleteDear student
DeleteYour comment has given me a lot of satisfaction.